IGCSE Simultaneous Equations: Linear & Quadratic Guide
Simultaneous equations involve finding the values of two variables (typically x and y) that satisfy two different equations at the same time. Graphically, this corresponds to finding the coordinates where two lines (or curves) intersect.
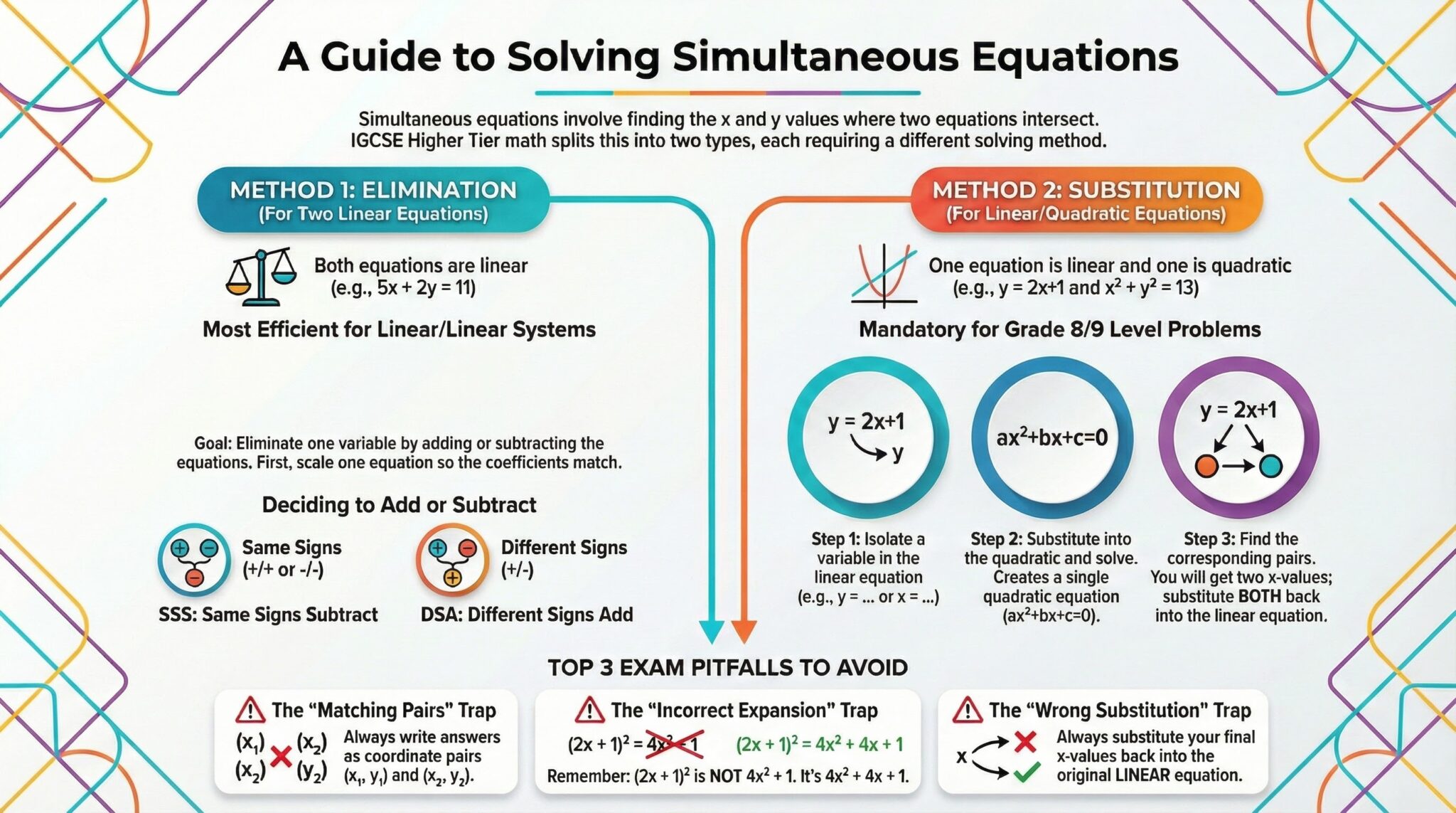
In the Edexcel IGCSE 4MA1 Higher Tier syllabus, this topic is split into two distinct skill levels: standard Linear/Linear systems and the challenging Linear/Quadratic pairs, which represent the "Grade 9" end of the spectrum.
This guide covers Topic 2.5 of the IGCSE Algebra Hub, providing detailed methods for both Elimination and Substitution.
1. Linear Simultaneous Equations (The Elimination Method)
When both equations are linear (powers of x and y are 1), the most efficient method is usually Elimination.
The Goal: Eliminate one variable by adding or subtracting the equations.
Method:
- Label the equations (1) and (2).
- Scale one or both equations so the coefficient (number in front) of either x or y is the same.
- Eliminate:
- If signs are the Same, Subtract the equations (SSS).
- If signs are Different, Add the equations.
- Solve the resulting single-variable equation.
- Substitute this value back into one of the original equations to find the second variable.
2. Linear and Quadratic Equations (The Substitution Method) (H)
This is a Higher Tier essential. When one equation is quadratic (contains x² or y² or xy), you must use the Substitution Method.
Method:
- Rearrange the linear equation to make one variable the subject (e.g., y = 3 - x).
- Substitute this expression into the quadratic equation.
- Expand and rearrange to form a quadratic equation equal to zero (ax² + bx + c = 0).
- Solve the quadratic (usually by factorising, sometimes formula).
- Substitute your x-values back into the linear equation to find the corresponding y-values.
Key Formulas & Mnemonics
Memorizing these simple rules will prevent sign errors during elimination.
| Condition | Action | Mnemonic |
|---|---|---|
| Same Signs (+/+ or -/-) | Subtract Equations | SSS (Same Signs Subtract) |
| Different Signs (+/-) | Add Equations | DSA (Different Signs Add) |
Step-by-Step Worked Examples
Question: Solve the simultaneous equations:
(1) 5x + 2y = 11
(2) 3x - y = 11
Methodology: Match the y-coefficients. Equation (2) has 1y, so we double it.
Solution:
- Multiply eq(2) by 2: 6x - 2y = 22 (3)
- Compare eq(1) and eq(3). Signs of y are different (+ and -), so ADD:
(5x + 6x) + (2y - 2y) = 11 + 22
11x = 33
x = 3 - Substitute x=3 into eq(2):
3(3) - y = 11
9 - y = 11
-y = 2 → y = -2
Answer: x = 3, y = -2.
Question: Solve the simultaneous equations:
(1) y = 2x + 1
(2) x² + y² = 13
Methodology: Use substitution. Equation (1) is already rearranged.
Solution:
- Substitute (1) into (2):
x² + (2x + 1)² = 13 - Expand Bracket: (2x + 1)(2x + 1) = 4x² + 2x + 2x + 1.
x² + (4x² + 4x + 1) = 13. - Collect and Simplify (Form Quadratic):
5x² + 4x - 12 = 0. - Solve Quadratic (Factorise):
(5x - 6)(x + 2) = 0.
x = 1.2 (or 6/5) and x = -2. - Find y (use the linear equation y = 2x + 1):
When x = 1.2: y = 2(1.2) + 1 = 3.4
When x = -2: y = 2(-2) + 1 = -3
Answer: Pair 1: (1.2, 3.4). Pair 2: (-2, -3).
Question: Solve:
x + y = 4
xy = 3
Solution:
- Rearrange linear: y = 4 - x.
- Substitute into quadratic: x(4 - x) = 3.
- Expand: 4x - x² = 3.
- Rearrange (move x² to make it positive):
x² - 4x + 3 = 0 - Factorise: (x - 3)(x - 1) = 0.
x = 3 or x = 1. - Find y: If x=3, y=1. If x=1, y=3.
Answer: Pairs are (3, 1) and (1, 3).
Real-World Application (Global Context)
Simultaneous equations allow us to model the intersection of physical paths.
Scenario: Trajectory Intersection
An air traffic control system monitors two objects. A weather balloon follows a linear path described by y = x + 10. A drone is flying in a circular holding pattern described by x² + y² = 100.
To determine if there is a risk of collision, the system solves these simultaneous equations to find the points of intersection. If real solutions exist, the paths cross, and the system must alert the drone operator to change altitude or course.
Exam Technique and Common Pitfalls
1. The "Matching Pairs" Trap
In quadratic questions, you will usually get two x values. You must substitute each one back to find its corresponding y value. A common error is mixing them up (e.g., pairing x₁ with y₂). Always write your answers as distinct pairs.
2. The "Square Difference" Trap
When expanding (2x + 1)², many students write 4x² + 1. This is incorrect. You must include the middle term (2ab). The correct expansion is 4x² + 4x + 1.
3. Choosing the Wrong Equation
Once you find your x-values in a quadratic problem, always substitute them back into the linear equation to find y. It is easier to calculate and avoids issues with square roots giving plus/minus options.
These linear/quadratic questions are often high-tariff (5-6 marks). Mastering complex algebra through structured practice is the best way to ensure you don't drop marks on the expansion or factorisation steps.
Summary Checklist and Next Steps
Checklist:
- [ ] I can use the Elimination Method for two linear equations.
- [ ] I can use the Substitution Method for linear/quadratic equations.
- [ ] I remember to expand brackets correctly (e.g., (x+3)²).
- [ ] I can solve the resulting quadratic equation (by factorising or formula).
- [ ] I remember to find the corresponding y-values for both x-values.
Practice Resources
Mastering simultaneous equations, especially linear-quadratic pairs, requires consistent practice. Use our dedicated worksheet to test your skills on both elimination and substitution methods.
Download Topic Worksheet: Simultaneous Equations (Linear & Quadratic)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
The substitution method relies heavily on your ability to solve quadratics. The next topic, Topic 2.6 Quadratic Equations, dives deeper into the Quadratic Formula and Completing the Square.