IGCSE Inequalities: Linear, Quadratic & Graphical Regions
Inequalities describe a range of values rather than a single specific answer. In the Edexcel IGCSE 4MA1 Higher Tier exam, you must be able to handle simple linear ranges (like speed limits), complex quadratic ranges, and graphical regions (shading the valid area on a graph).
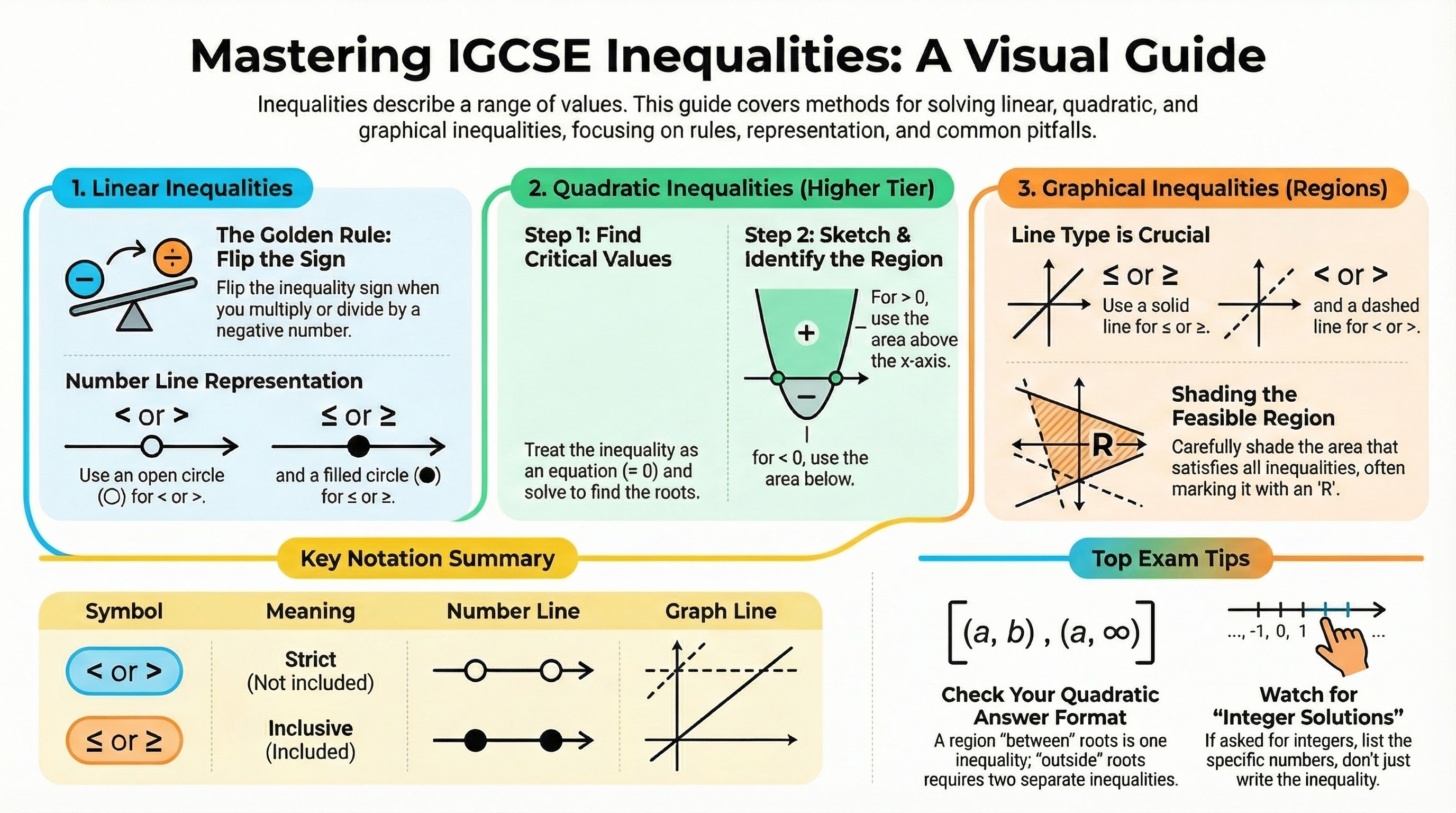
This guide covers Topic 2.7 of the IGCSE Algebra Hub, breaking down the rules for linear inequalities, the logic for quadratics, and the visual method for graphical regions.
1. Linear Inequalities
Solving a linear inequality is almost identical to solving linear equations. You use the Balance Method to isolate x.
The Golden Rule: Flipping the Sign
There is one crucial difference: If you multiply or divide both sides by a NEGATIVE number, you must FLIP the inequality sign.
- Example: -2x > 10
- Divide by -2: x < -5 (Sign flips from > to <).
Representation on a Number Line
- Open Circle (○): Use for strict inequalities (< or >). The value is NOT included.
- Filled Circle (●): Use for inclusive inequalities (≤ or ≥). The value IS included.
2. Quadratic Inequalities (H)
This is a Higher Tier essential. Unlike linear inequalities, you cannot simply "solve for x". You must consider the shape of the graph.
Method (The Critical Values Approach):
- Treat as an Equation: Replace the inequality sign with an equals sign (x² - 5x + 6 = 0).
- Find Critical Values: Solve for x to find the "roots" (where the graph crosses the x-axis).
- Sketch the Graph: Draw a quick U-shaped curve crossing the x-axis at your critical values.
- Identify the Region:
- If > 0 (greater than), you want the parts above the x-axis (Outside the roots).
- If < 0 (less than), you want the part below the x-axis (Between the roots).
3. Graphical Inequalities (Regions)
This involves shading regions on a coordinate grid defined by multiple lines (e.g., y ≤ x + 1).
Conventions:
- Solid Line: For inclusive inequalities (≤, ≥). The line itself is part of the region.
- Dashed Line: For strict inequalities (<, >). The line is a boundary but not included.
- Shading: Read the question carefully. Some ask to shade the region that satisfies the inequalities; others ask to shade the region that does not (leaving the solution unshaded). Edexcel usually asks to mark the correct region with an R.
Key Notation Summary
| Symbol | Meaning | Number Line | Graph Line |
|---|---|---|---|
| < | Less than | Open Circle | Dashed |
| > | Greater than | Open Circle | Dashed |
| ≤ | Less than or equal | Filled Circle | Solid |
| ≥ | Greater than or equal | Filled Circle | Solid |
Step-by-Step Worked Examples
Question: Solve 5x - 3 < 2x + 12.
Methodology: Use the balance method. Move the smaller x term first.
Solution:
- Subtract 2x from both sides:
3x - 3 < 12 - Add 3 to both sides:
3x < 15 - Divide by 3 (Positive, so sign stays):
x < 5
Answer: x < 5.
Question: Solve x² - 3x - 10 ≥ 0.
Methodology: Use Critical Values.
Solution:
- Solve Equation: x² - 3x - 10 = 0.
Factorise: (x - 5)(x + 2) = 0.
Critical Values: x = 5 and x = -2. - Sketch Graph: A U-shaped curve crossing at -2 and 5.
- Analyze Region: We want ≥ 0 (Above the axis).
This corresponds to the two tails moving away from the center. - Write Inequality: x ≤ -2 or x ≥ 5.
Answer: x ≤ -2 or x ≥ 5.
Question: Write down the three inequalities that define the shaded region R.
(Assume visual: A triangle bounded by the x-axis, the line x=2, and the line y=x).
Solution:
- Boundary 1 (Bottom): The region is above the x-axis (y=0).
Inequality: y ≥ 0. - Boundary 2 (Right): The region is to the left of the vertical line x=2.
Inequality: x ≤ 2. - Boundary 3 (Diagonal): The region is below the line y=x.
Inequality: y ≤ x.
Answer: y ≥ 0, x ≤ 2, y ≤ x.
Real-World Application (Global Context)
Inequalities are used in Linear Programming to optimize resources under constraints.
Scenario: Manufacturing Constraints
A factory produces two products, A and B.
• Machine 1 can run for at most 100 hours.
• Product A takes 2 hours, Product B takes 1 hour: 2A + B ≤ 100.
• Machine 2 can run for at most 80 hours.
• Product A takes 1 hour, Product B takes 3 hours: A + 3B ≤ 80.
• Production cannot be negative: A ≥ 0, B ≥ 0.
By graphing these inequalities, the factory manager identifies the "Feasible Region". The optimal production numbers (for maximum profit) will always lie at one of the vertices (corners) of this region.
Exam Technique and Common Pitfalls
1. The "Combined Inequality" Mistake
For quadratic inequalities, checking if the answer is "And" vs "Or" is vital.
• If x is between -2 and 5, write: -2 < x < 5. (One continuous region).
• If x is outside, you MUST write two separate inequalities: x < -2 OR x > 5. Writing -2 > x > 5 is mathematically nonsense.
2. Strict vs. Inclusive
Always check if the line should be dashed or solid.
• "Greater than" (>) = Dashed Line.
• "Greater than or equal to" (≥) = Solid Line.
Missing this detail costs easy marks.
3. Integer Solutions
Read the question carefully. If it asks for "integer values for x", do not just leave the answer as an inequality (x < 4). You must list them (..., 1, 2, 3).
Graphical inequalities are visual and require precision. Mastering high-tariff inequality questions ensures you don't lose marks on shading or line types.
Summary Checklist and Next Steps
Checklist:
- [ ] I can solve linear inequalities and flip the sign when dividing by a negative.
- [ ] I can represent inequalities on a number line (open vs closed circles).
- [ ] (H) I can solve quadratic inequalities by finding critical values and sketching the graph.
- [ ] I can draw lines for graphical inequalities (solid vs dashed).
- [ ] I can identify and shade the region R that satisfies multiple inequalities.
Practice Resources
Mastering inequalities, especially quadratic and graphical regions, requires consistent practice. Use our dedicated worksheet to test your skills on shading regions and solving complex ranges.
Download Topic Worksheet: Inequalities (Linear, Quadratic & Graphical)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
This concludes the main algebraic solving techniques. The final topic in this section is Topic 2.8 Algebraic Proof, where you will use your manipulation skills to prove mathematical statements logically.