IGCSE Sequences: Linear & Quadratic Nth Term Formulas
A sequence is an ordered list of numbers that follows a specific rule. In the Edexcel IGCSE 4MA1 Higher Tier exam, you are required to find the algebraic formula—the nth term—that generates any number in the sequence. This guide covers Topic 3.1 of the IGCSE Functions & Graphs Hub.
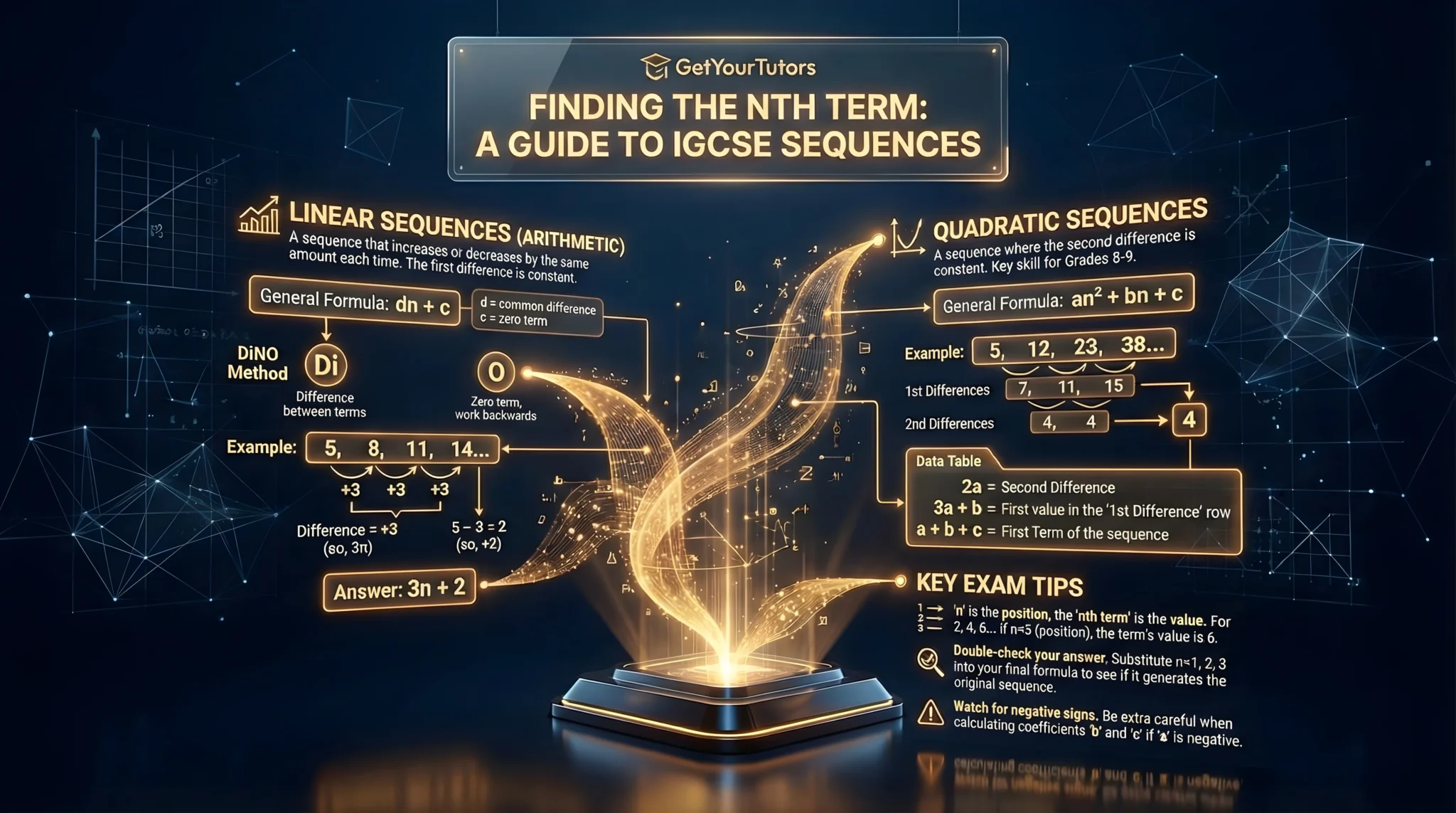
We will start with simple Linear Sequences (constant difference) and then master the advanced "Algebraic Difference Method" for Quadratic Sequences (constant second difference), a key skill for achieving Grades 8-9.
1. Linear Sequences (Arithmetic Progressions)
A linear sequence increases or decreases by the same amount each time. The formula is always in the form dn + c.
The DiNO Method
A helpful way to remember the steps:
- Di (Difference): Find the gap between terms. This becomes the number in front of n (e.g., 3n).
- N (n): Write 'n' next to the difference.
- O (Zero term): Work backwards to find the term before the first one. This is the constant c.
2. Quadratic Sequences (H)
If the first difference is not constant, but the second difference is, the sequence is quadratic. The formula is an² + bn + c.
The Algebraic Difference Method
To find the coefficients a, b, and c, you should memorize these three standard results derived from the first three terms of any quadratic sequence.
| Value to Find | Formula to Memorize |
|---|---|
| Second Difference | 2a = [Second Diff] |
| First Difference (between term 1 and 2) | 3a + b = [First Diff] |
| First Term (n=1) | a + b + c = [First Term] |
Step-by-Step Worked Examples
Question: Find the nth term of the sequence: 5, 8, 11, 14...
Methodology: Use the DiNO method.
Solution:
- Difference (Di): +3. Write 3n.
- Zero Term (O): Work backwards from 5. (5 - 3 = 2). The constant is +2.
- Combine: nth term = 3n + 2.
Answer: 3n + 2.
Question: Find the nth term of the sequence: 5, 12, 23, 38, 57...
Methodology: Find the differences and solve the algebraic equations for a, b, and c.
Solution:
- Find Differences:
Sequence: 5, 12, 23, 38
1st Diff: 7, 11, 15
2nd Diff: 4 (Constant). - Find 'a' (2a = 2nd Diff):
2a = 4 → a = 2. - Find 'b' (3a + b = 1st Diff):
Use the *first* number of the 1st diff row (7).
3(2) + b = 7 → 6 + b = 7 → b = 1. - Find 'c' (a + b + c = 1st Term):
Use the *first* number of the sequence (5).
2 + 1 + c = 5 → 3 + c = 5 → c = 2. - Combine:
nth term = 2n² + 1n + 2.
Answer: 2n² + n + 2.
Question: The nth term of a sequence is n² + 4n - 5. Determine if 150 is a term in this sequence.
Methodology: Set the formula equal to 150 and attempt to solve the quadratic. If 'n' is a positive integer, it is a term.
Solution:
- Set up the equation:
n² + 4n - 5 = 150 - Rearrange to equal zero:
n² + 4n - 155 = 0 - Solve for n (using Quadratic Formula):
a=1, b=4, c=-155.
n = -4 ± √(16 - 4(1)(-155))2
n = -4 ± √(636)2 - Evaluate:
√636 is approx 25.2. Since the result is not a whole number, n is not an integer.
Answer: No, 150 is not a term.
Real-World Application (Global Context)
Sequences are fundamental in computer science for analyzing the efficiency of algorithms (Big O notation).
Scenario: Algorithm Efficiency
A software engineer tests a sorting algorithm. She records the time taken (in ms) to sort lists of increasing size (n=1, 2, 3...).
Times: 5, 20, 45, 80...
The second difference is constant (+10), meaning the time complexity is quadratic (Formula: T = 5n²). This tells the engineer that doubling the data size will quadruple the processing time—critical information for designing scalable global systems like Google Search or Amazon's databases.
Exam Technique and Common Pitfalls
1. Confusing n with the Term
Remember: n is the position (1st, 2nd...). The nth term is the value.
Example: In 2, 4, 6... for the 3rd term, n=3, value=6.
2. The Sign Error in Quadratics
When finding coefficients b and c, be very careful with negative numbers.
If 2nd diff is -2, then 2a = -2 so a = -1.
If 3a + b = 1st diff (let's say 4), then 3(-1) + b = 4 → -3 + b = 4 → b = 7.
3. "Generate the Sequence" Check
Once you have your formula (e.g., 2n² + 1), substitute n=1, 2, 3 back into it. If you get the original numbers (3, 9, 19...), you know for certain you have full marks. This is a key habit for mastering Grade 9 sequence patterns.
Summary Checklist and Next Steps
Checklist:
- [ ] I can use the DiNO method for linear sequences.
- [ ] I can calculate the first and second differences of a sequence.
- [ ] I have memorized the quadratic solver equations (2a, 3a+b, a+b+c).
- [ ] I can solve quadratic equations to check if a number belongs to a sequence.
Practice Resources
Mastering the nth term for linear and quadratic sequences requires practice. Use our dedicated worksheet to test your skills on finding formulae and solving sequence problems.
Download Topic Worksheet: Sequences (Linear & Quadratic Nth Term)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
Now that you can describe patterns algebraically, the next logical step is Topic 3.2 Function Notation, where we replace 'n' with 'x' and treat these rules as functions.