The Ultimate Guide to IGCSE Sequences, Functions, and Graphs
If Algebra is the language of mathematics, Graphs are its picture. Topic 3: Sequences, Functions, and Graphs bridges the gap between abstract Algebraic foundations and their visual representation.
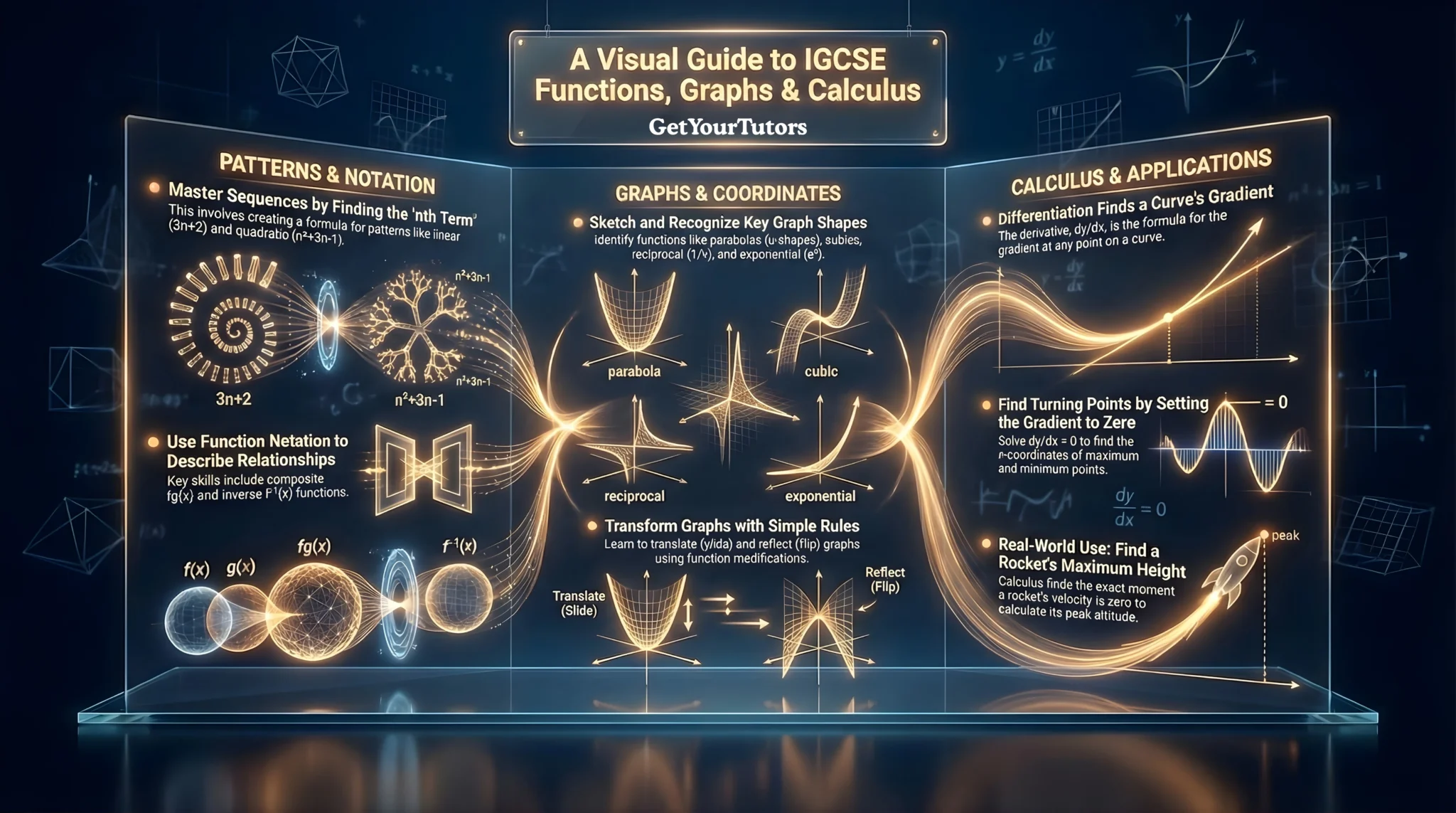
In the Edexcel IGCSE 4MA1 Higher Tier syllabus, this section introduces some of the most advanced concepts you will encounter, including Function Notation, Calculus (Differentiation), and Graph Transformations. These topics are the gateway to A-Level mathematics and require a deep conceptual understanding.
Deep Dive: The Structure of Topic 3
We have organized this vast topic into four logical pillars. Click through to the detailed guides below for deep practice on specific skills.
1. Patterns and Notation (3.1 – 3.2)
Before drawing graphs, you must understand how numbers behave in patterns and how we write relationships formally.
3.1 Sequences (H)
Sequences are ordered lists of numbers that follow a specific rule. The Higher Tier requires you to find the "nth term" formula.
- Linear Sequences: Constant difference (e.g., 3n + 2).
- Quadratic Sequences (H): Constant second difference (e.g., n² + 3n - 1). You must solve for coefficients a, b, and c.
3.2 Function Notation (H)
Functions are machines that take an input (x) and give an output (y or f(x)). This notation is crucial for advanced maths.
- Composite Functions fg(x): Applying one function inside another.
- Inverse Functions f⁻¹(x): Reversing the operations of a function.
- Domain and Range: Understanding the valid inputs and possible outputs.
2. Graphs and Coordinates (3.3 – 3.5, 3.8)
This section deals with visualizing equations on a coordinate grid.
3.3 Linear Graphs
Mastering straight lines (y = mx + c).
- Gradient (m) and Intercept (c): Calculating slope and position.
- Parallel and Perpendicular (H): Using gradients (m₁ = m₂ vs m₁ × m₂ = -1) to find equations of related lines.
3.4 Graphs of Functions (H)
You must recognize and sketch non-linear shapes.
- Quadratics: Parabolas (u-shapes). Finding turning points.
- Other Functions: Cubic, Reciprocal (1/x), Exponential (aˣ), and Trigonometric graphs.
3.5 Solving Equations Graphically
Using the intersection points of two graphs to solve equations like x² = 2x + 1.
Read the detailed guide on Graphical Solutions →3. Calculus and Applications (3.6 – 3.7)
This is the introduction to A-Level style mathematics, analyzing rates of change.
3.6 Real-Life Graphs
Interpreting Distance-Time and Velocity-Time graphs to calculate speed, acceleration, and distance travelled (area under the graph).
Read the detailed guide on Real-Life Graphs →3.7 Calculus: Differentiation (H)
A powerful tool for finding the gradient of a curve at any point.
- Differentiation: The rule for differentiating axⁿ to find dy/dx.
- Gradients: Calculating the exact gradient of a curve at a specific point.
- Turning Points: Finding Maximum and Minimum points by setting dy/dx = 0.
- Kinematics (H): Applying calculus to displacement (s), velocity (v), and acceleration (a).
3.8 Transformations of Graphs (H)
Modifying the input or output of a function to move its graph.
- Translations: f(x) + a (vertical) vs f(x + a) (horizontal).
- Reflections: -f(x) (x-axis) vs f(-x) (y-axis).
Synthesized Worked Example (Grade 9 Level)
High-tariff questions often combine functions, calculus, and graphs.
A curve has the equation y = 2x³ - 3x² - 12x + 5.
a) Find the coordinates of the turning points.
b) Determine whether each turning point is a maximum or a minimum.
SolutionPart (a): Find Turning Points
1. Differentiate to find the gradient function:
dydx = 6x² - 6x - 12.
2. Set gradient to zero for turning points:
6x² - 6x - 12 = 0.
3. Simplify (divide by 6) and factorise:
x² - x - 2 = 0 → (x - 2)(x + 1) = 0.
So, x = 2 or x = -1.
4. Find y-coordinates:
At x = 2: y = 2(8) - 3(4) - 12(2) + 5 = -15. Point: (2, -15).
At x = -1: y = 2(-1) - 3(1) - 12(-1) + 5 = 12. Point: (-1, 12).
Part (b): Determine Nature
Use the Second Derivative (d²ydx²) test:
Differentiate dy/dx: d²ydx² = 12x - 6.
At x = 2: 12(2) - 6 = 18 (>0). Positive means Minimum.
At x = -1: 12(-1) - 6 = -18 (<0). Negative means Maximum.
Answer: (2, -15) is a Minimum. (-1, 12) is a Maximum.
Video Masterclass: Visualizing Calculus & The Rocket Trajectory
Real-World Application (Global Context)
Calculus allows us to optimize real-world systems.
Scenario: Rocket Trajectory
A model rocket is launched vertically. Its height h meters after t seconds is given by h = 30t - 5t².
To find the maximum height reached, we use differentiation (Kinematics):
- Velocity v = dhdt = 30 - 10t.
- At maximum height, velocity is zero (v=0).
- 30 - 10t = 0 → 10t = 30 → t = 3 seconds.
- Max Height = 30(3) - 5(3)² = 90 - 45 = 45 meters.
This principle allows engineers to calculate peak altitudes and fuel efficiency for aircraft and spacecraft.
Exam Strategies for IGCSE Graphs
1. Sketching vs. Plotting
Know the difference:
- Plot: Use a table of values and precise points on a grid.
- Sketch: Draw the general shape and label key points (roots, y-intercept, turning points).
2. The "dy/dx" Interpretation
Always remember: dy/dx IS the gradient. If a question asks for the "rate of change" or "gradient of the tangent," you differentiate.
3. Function Notation Precision
Be careful with fg(x). It means put g(x) INSIDE f(x). It is almost never the same as gf(x).
This section contains some of the most technically demanding content in the syllabus. Expert graphing and calculus tuition can make the difference between confusing these abstract concepts and mastering them for full marks.
Summary and Next Steps
Mastering Topic 3 gives you the ability to visualize mathematics. You now have the tools to predict patterns (Sequences), model relationships (Functions), and analyze rates of change (Calculus).
Practice with IGCSE Maths Worksheets
Mastering functions and calculus requires consistent practice. Consolidate your learning across all these sub-topics with our comprehensive library of worksheets and model answers.
Get Free IGCSE Edexcel Maths Worksheets & Answers
What's Next?
The final major pillar of the syllabus is Topic 4: Geometry and Trigonometry, where you will apply your logical reasoning to shapes, angles, and 3D space.