IGCSE Real-Life Graphs: Distance, Velocity & Acceleration
Graphs are not just abstract lines on a grid; they are powerful tools used to model real-world motion. In the Edexcel IGCSE 4MA1 Higher Tier syllabus, you must be able to interpret and perform calculations from two specific types of graphs: Distance-Time and Velocity-Time graphs.
This guide covers Topic 3.6 of the IGCSE Functions & Graphs Hub. Mastering this topic links directly to IGCSE Physics concepts, reinforcing your understanding of speed, velocity, and acceleration.
1. Distance-Time Graphs
A Distance-Time graph shows how far an object has travelled from a starting point over a period of time.
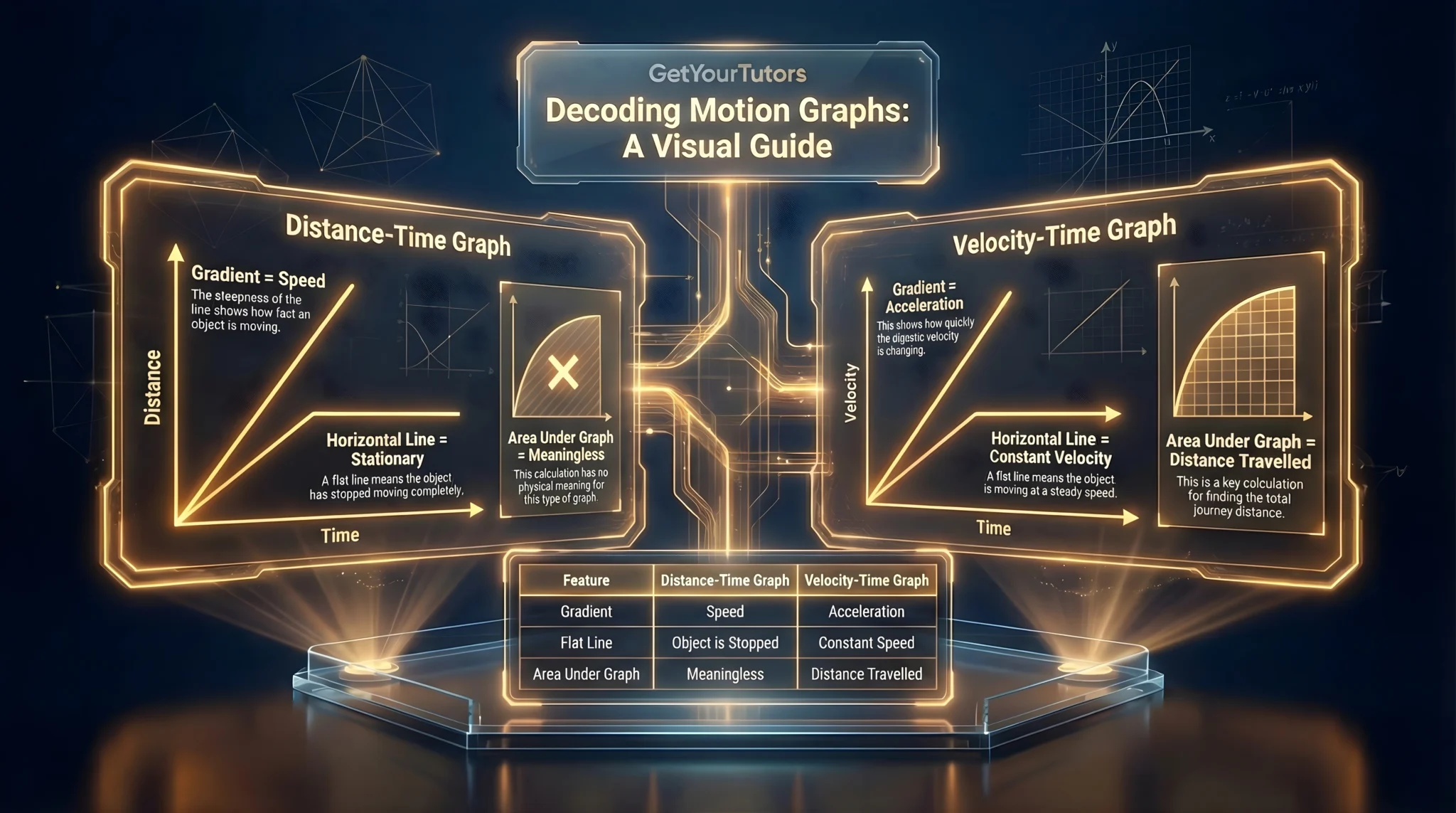
Key Features
- Gradient = Speed. The steeper the line, the faster the speed.
- Horizontal Line = Stationary. The object has stopped (distance is not changing).
- Straight Line = Constant Speed.
- Curved Line = Acceleration/Deceleration. (Changing speed).
Calculating Speed
To calculate speed from the graph, find the gradient of the line.
Speed = Change in Distance (Vertical)Change in Time (Horizontal)
2. Velocity-Time Graphs
A Velocity-Time graph shows how the speed of an object changes over time. This is more complex and yields more information.
Key Features
- Gradient = Acceleration. How quickly the speed is changing.
- Positive gradient = Acceleration.
- Negative gradient = Deceleration.
- Horizontal line = Constant Velocity (Zero acceleration).
- Area Under Graph = Distance Travelled. This is the most common high-mark question. You split the area into geometric shapes (rectangles and triangles/trapeziums) to calculate the total distance.
Summary Table: What the Graph Tells You
| Feature | Distance-Time Graph | Velocity-Time Graph |
|---|---|---|
| Y-Axis | Distance (m, km) | Velocity (m/s, km/h) |
| Gradient | Speed | Acceleration |
| Flat Line | Stopped | Constant Speed |
| Area Under Graph | Meaningless | Distance Travelled |
Step-by-Step Worked Examples
Question: A cyclist travels 20km in 1 hour, stops for 30 minutes, then travels a further 30km in 1.5 hours. Calculate their average speed for the whole journey.
Solution:
- Total Distance: 20km + 0km (stop) + 30km = 50km.
- Total Time: 1h + 0.5h (30 mins) + 1.5h = 3 hours.
- Average Speed: Total DistanceTotal Time = 503 = 16.7 km/h (to 3 s.f.).
Answer: 16.7 km/h.
Question: On a velocity-time graph, a car accelerates from 10 m/s to 30 m/s in 5 seconds. Calculate the acceleration.
Methodology: Acceleration is the gradient of the line.
Solution:
- Change in Velocity (Rise): 30 - 10 = 20 m/s.
- Change in Time (Run): 5 seconds.
- Gradient: 205 = 4.
Answer: 4 m/s².
Question: A train starts from rest, accelerates to 15 m/s in 10 seconds, travels at a constant speed for 30 seconds, then decelerates to rest in 10 seconds. Calculate the total distance travelled.
Methodology: Calculate the Area Under the Graph. This shape forms a Trapezium.
Solution:
- Area A (Triangle): 0-10s.
Area = 0.5 × base × height = 0.5 × 10 × 15 = 75m. - Area B (Rectangle): 10-40s.
Area = base × height = 30 × 15 = 450m. - Area C (Triangle): 40-50s.
Area = 0.5 × 10 × 15 = 75m. - Total Distance: 75 + 450 + 75 = 600m.
Alternative (Trapezium Rule): Area = 0.5(a + b)h = 0.5(30 + 50) × 15 = 0.5(80)(15) = 600m.
Answer: 600 meters.
Real-World Application (Global Context)
These graphs are essential for analyzing athletic performance and vehicle safety.
Scenario: Usain Bolt's 100m Sprint
Sports scientists analyze the Velocity-Time graph of a sprinter. The graph is not a straight line; it curves as the runner accelerates out of the blocks.
• The steepest gradient shows where they have the most explosive power (highest acceleration).
• The peak of the curve shows their top speed.
• The area under the curve must equal exactly 100 meters.
By studying these graphs, coaches can determine if an athlete needs to work on their start (initial gradient) or their endurance (maintaining the flat line of constant velocity).
Exam Technique and Common Pitfalls
1. Mixing Up the Graphs
Check the y-axis labels immediately!
• If y = Distance, a horizontal line means stopped.
• If y = Velocity, a horizontal line means moving at steady speed.
2. Unit Conversions
Ensure your units match. If speed is in km/h but time is in minutes, you must convert minutes to hours (divide by 60) before calculating. This is a common trap in "Average Speed" questions.
3. Negative Gradient
On a Velocity-Time graph, a negative gradient (line going down) means deceleration. The value of acceleration is negative (e.g., -2 m/s²), but deceleration is often stated as positive (2 m/s²). Read the question to see which term is required.
Mastering kinematics calculations ensures you don't drop marks on unit conversions or area calculations.
Summary Checklist and Next Steps
Checklist:
- [ ] I can calculate speed from the gradient of a Distance-Time graph.
- [ ] I can calculate acceleration from the gradient of a Velocity-Time graph.
- [ ] I can calculate total distance by finding the area under a Velocity-Time graph.
- [ ] I check the units (e.g., minutes vs hours) before calculating.
Practice Resources
Mastering real-life graphs requires practice, especially in interpreting gradients and calculating areas under curves. Use our dedicated worksheet to test your skills on distance-time and velocity-time graphs.
Download Topic Worksheet: Real-Life Graphs (Distance, Velocity & Acceleration)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
You have learned to find gradients and rates of change using geometry. The next level involves doing this algebraically for any curve. Move on to Topic 3.7 Calculus: Differentiation to learn the ultimate tool for rates of change.