IGCSE Maths: Mastering Ratio, Direct and Inverse Proportion (H)
Ratio and Proportion are fundamental concepts in the IGCSE Number System that describe how quantities relate to one another. While basic ratio skills are covered in earlier years, the Edexcel IGCSE 4MA1 Higher Tier demands a rigorous algebraic approach. You must be able to manipulate ratios algebraically (x:y:z) and model complex relationships using Direct and Inverse Proportion laws.
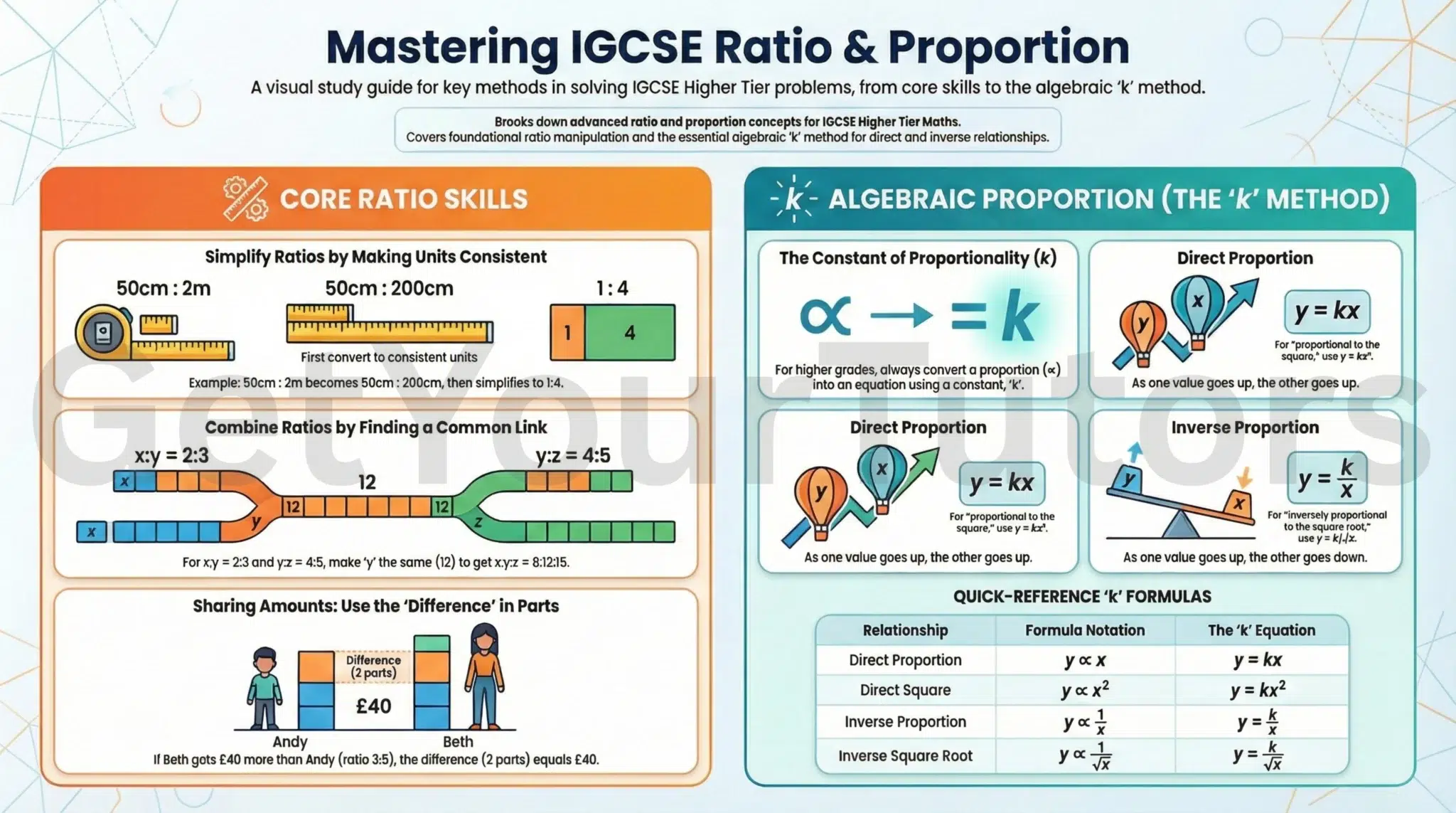
This guide provides a definitive walkthrough of Topic 1.8, moving from core simplification to the advanced "constant of proportionality (k)" method required for Grades 7-9.
Understanding Ratio: Core Concepts
A ratio compares the size of two or more quantities. It does not contain units (as long as the quantities compared have the same units).
1. Simplification and Unit Consistency
Like fractions, ratios should always be simplified to their lowest terms by dividing all parts by the Highest Common Factor (HCF).
- Rule: You can only simplify if units are the same.
- Example: Simplify 50cm : 2m.
- Convert to same units: 50cm : 200cm.
- Simplify (divide by 50): 1 : 4.
2. The Unitary Form (1:n)
Exam questions often ask you to write a ratio in the form 1:n. This simply means the first number must be 1. You achieve this by dividing both sides by the first number.
- Example: Write 4:5 in the form 1:n.
- Divide both sides by 4.
- 1 : 1.25. (Here, n = 1.25).
3. Combining Ratios (x:y:z) (H)
A common Higher Tier question involves combining two separate ratios into one.
- Given: x:y = 2:3 and y:z = 4:5.
- Task: Find x:y:z.
- Method: Make the "linking variable" (y) the same number in both ratios (find the Lowest Common Multiple).
- Multiply first ratio by 4 → x:y = 8:12.
- Multiply second ratio by 3 → y:z = 12:15.
- Result: 8:12:15.
Dividing in a Ratio: Total vs. Difference
To share an amount in a given ratio, you must identify if you are working with the Total or a Difference.
- Total Amount: Add the parts (a+b) to find the "total shares". Divide the total money by this number.
- Difference/Specific Share: Do not add the parts. If the question says "A gets £10 more than B", find the difference in parts (a-b) and equate it to £10.
Video Lesson: Mastering Ratio & The 'k' Method for Proportion
Direct and Inverse Proportion (Algebraic Method)
In the Higher Tier, proportion is modeled using algebra. You must introduce a constant of proportionality, denoted by k.
Direct Proportion (y ∝ x)
If y is directly proportional to x, as x increases, y increases at a constant rate.
- Formula: y = kx
Note: Higher Tier questions often involve powers.
- "y is directly proportional to the square of x" → y = kx2.
Inverse Proportion (y ∝ 1x)
If y is inversely proportional to x, as x increases, y decreases.
- Formula: y = kx
Note: This also involves powers and roots.
- "y is inversely proportional to the square root of x" → y = k√x.
Key Formulas Summary
To gain the first Method Mark (M1) in any algebraic proportion question, you must immediately convert the "proportional to" symbol (∝) into an equation using k.
| Relationship | Notation | Equation (The "k" Formula) |
|---|---|---|
| Direct | y ∝ x | y = kx |
| Direct Square | y ∝ x2 | y = kx2 |
| Inverse | y ∝ 1x | y = kx |
| Inverse Root | y ∝ 1√x | y = k√x |
Step-by-Step Worked Examples
Question: Andy and Beth share money in the ratio 3:5. Beth gets £40 more than Andy. Work out how much money was shared in total.
Methodology: The £40 represents the difference in shares, not the total.
Solution:
- Find difference in parts: 5 - 3 = 2 parts.
- Calculate value of 1 part:
2 parts = £40.
1 part = £20. - Calculate Total:
Total parts = 3 + 5 = 8.
Total Money = 8 × 20 = £160.
Answer: £160.
Question: M is directly proportional to the square of r. When r = 5, M = 200.
a) Find a formula for M in terms of r.
b) Calculate the value of M when r = 8.
Solution:
- Set up equation (M1): M ∝ r2 → M = kr2.
- Find k:
Substitute M=200, r=5.
200 = k × 52
200 = 25k
k = 8. - Write Formula: M = 8r2 (A1).
- Solve part (b):
M = 8 × 82
M = 8 × 64 = 512.
Answer: 512.
Question: y is inversely proportional to the square root of x. When x = 16, y = 5. Find the value of x when y = 2.
Solution:
- Set up equation (M1): y ∝ 1√x → y = k√x.
- Find k:
5 = k√16
5 = k4
k = 20.
Formula: y = 20√x. - Solve for x: (Requires rearranging formulae)
2 = 20√x
Multiply by √x: 2√x = 20.
Divide by 2: √x = 10.
Square both sides: x = 100.
Answer: x = 100.
Real-World Application (Global Context)
Inverse proportion is a fundamental concept in physics, explaining phenomena such as light intensity and gravitational force.
Scenario: The Inverse Square Law (Light Intensity)
The intensity (I) of light from a source is inversely proportional to the square of the distance (d) from the source. This is crucial for photographers, stage lighting technicians, and astronomers.
Problem: A studio light has an intensity of 800 lux at a distance of 2 meters. What is the intensity if the light is moved to a distance of 4 meters?
Solution:
- Model: I = kd2.
- Find k:
800 = k22 → 800 = k4.
k = 3200.
Formula: I = 3200d2. - Calculate new Intensity:
I = 320042 = 320016 = 200.
Answer: 200 lux. (Note: Doubling the distance reduced the intensity by a factor of 4).
Exam Technique and Common Pitfalls
Securing full marks on proportion questions requires algebraic discipline.
1. The "Square" vs "Square Root" Trap
Read the question twice. Confusing x2 with √x is the most common cause of lost marks in this topic.
- "Proportional to the square" → x2
- "Proportional to the square root" → √x
2. Finding k is Mandatory
Even if the question doesn't explicitly ask "Find the formula for y in terms of x", you must find k to answer the final part. Write down your formula clearly (y=kx...) to secure method marks. This is a core part of mastering high-tariff algebraic questions.
3. Combining Ratios
When asked to find a:c given a:b and b:c, do not just guess. Use the LCM method to make the middle term (b) equal in both ratios before combining.
Summary Checklist and Next Steps
Checklist:
- [ ] I can simplify ratios and convert them to the 1:n form.
- [ ] I can solve ratio problems involving the difference between shares.
- [ ] I can combine two ratios (x:y and y:z) into a single ratio.
- [ ] I can set up equations for Direct Proportion (y=kx, y=kx2).
- [ ] I can set up equations for Inverse Proportion (y=k/x, y=k/√x).
- [ ] I can calculate the constant k and use it to solve for unknowns.
Practice Resources
Mastering ratio and proportion, especially the algebraic "k-method" for direct and inverse proportion, requires practice. Use our dedicated worksheet to test your skills on these essential problem-solving questions.
Download Topic Worksheet: Ratio, Proportion & Direct/Inverse
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
This completes the core Number skills. You are now ready for Topic 1.9 Degree of Accuracy, dealing with bounds and error intervals. Furthermore, the algebraic skills mastered here are the direct foundation for Topic 4.5 Similar Shapes and Scale Factors in Geometry.