IGCSE Quadratics: Factorising, Formula & Completing the Square
A quadratic equation is an equation where the highest power of the variable is 2 (e.g., x²). These equations model trajectories in physics, profit curves in economics, and geometric areas. In the Edexcel IGCSE 4MA1 Higher Tier exam, solving quadratics is a guaranteed topic. Unlike linear equations which have one solution, quadratics can have two, one, or no real solutions.
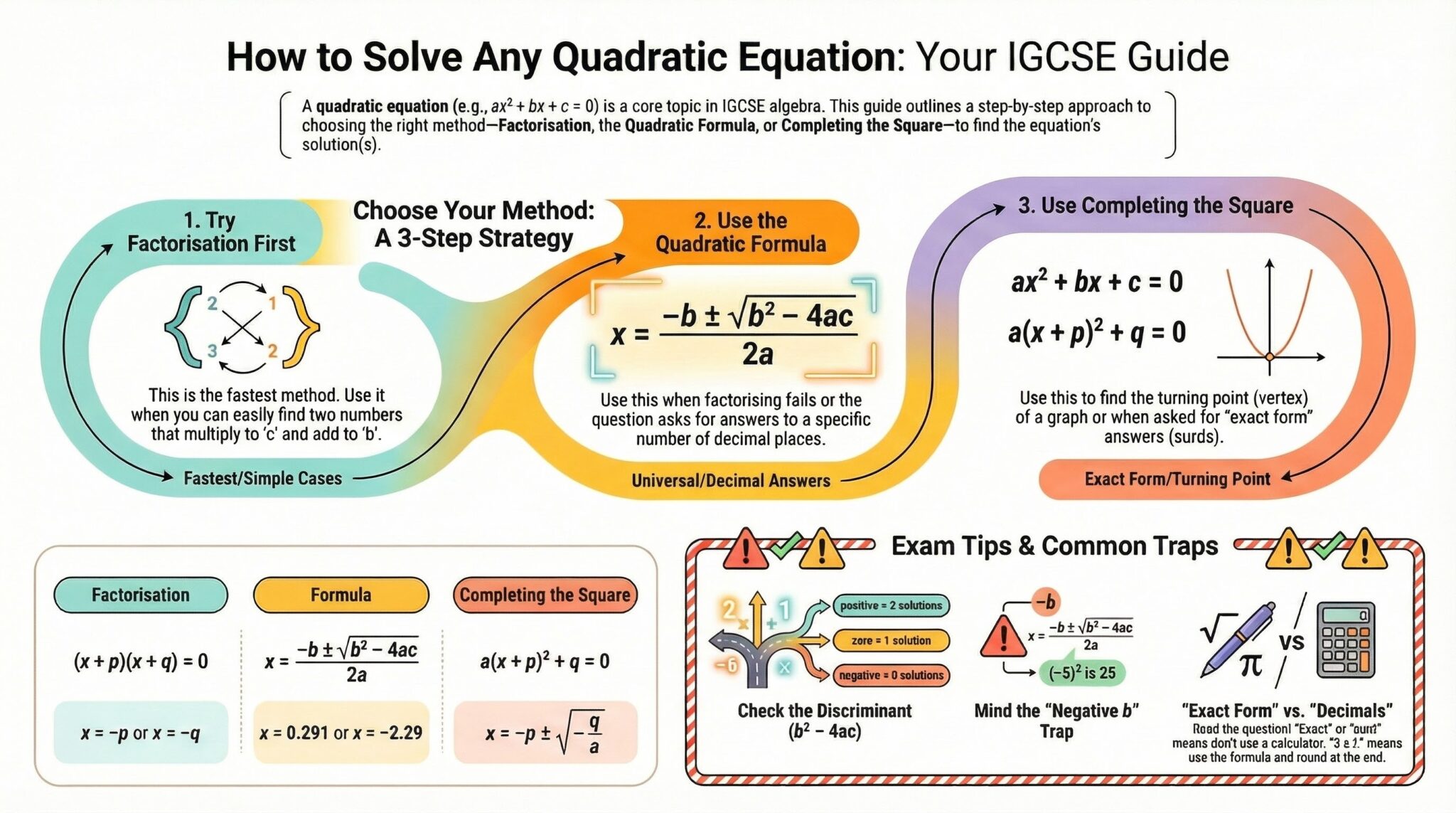
This guide covers Topic 2.6 of the IGCSE Algebra Hub, detailing the three essential methods you must know: Factorisation, the Quadratic Formula, and Completing the Square.
1. Solving by Factorisation
This is the fastest method and should always be your first attempt. It relies on the "Zero Product Property": if two things multiply to give zero, one of them must be zero.
Method:
- Rearrange the equation so it equals zero: ax² + bx + c = 0.
- Factorise the quadratic into two brackets: (x + p)(x + q) = 0.
- Set each bracket to 0 and solve for x.
Example: (x - 3)(x + 5) = 0 → x = 3 or x = -5.
2. The Quadratic Formula (H)
When a quadratic does not factorise easily (or at all), or when the question asks for answers to "3 significant figures" or "2 decimal places," you must use the formula.
x = -b ± √(b² - 4ac)2a
Critical Check: The value inside the square root (b² - 4ac) is called the Discriminant.
• If positive: 2 real solutions.
• If zero: 1 solution (repeated root).
• If negative: No real solutions (Math error).
3. Completing the Square (H)
This method converts ax² + bx + c into the form a(x + p)² + q. It is a powerful tool used to solve equations and, importantly, to find the coordinates of the turning point (vertex) of quadratic graphs.
Method (for x² + bx + c):
- Halve the coefficient of x (b) to get p. Write (x + p)².
- Subtract the square of p: -(p)².
- Add the original constant c.
- Solve by rearranging and using square roots.
Step-by-Step Worked Examples
Question: Solve x² - 2x - 15 = 0.
Methodology: Find two numbers that multiply to -15 and add to -2.
Solution:
- Factors of -15: (1, -15), (3, -5)... 3 and -5 add to -2.
- Factorise: (x + 3)(x - 5) = 0.
- Solve bracket 1: x + 3 = 0 → x = -3.
- Solve bracket 2: x - 5 = 0 → x = 5.
Answer: x = -3, x = 5.
Question: Solve 3x² + 6x - 2 = 0. Give your answers to 3 significant figures.
Methodology: "3 s.f." indicates the formula is required. a=3, b=6, c=-2.
Solution:
- Substitute into formula:
x = -6 ± √(6² - 4(3)(-2))2(3) - Simplify the discriminant (Watch the double negative!):
36 - (-24) = 36 + 24 = 60.
x = -6 ± √606 - Calculate both paths:
x₁ = (-6 + √60) ÷ 6 = 0.29099...
x₂ = (-6 - √60) ÷ 6 = -2.29099... - Round to 3 s.f.:
Answer: x = 0.291 or x = -2.29.
Question: Express x² - 8x + 5 in the form (x + a)² + b. Hence solve x² - 8x + 5 = 0 in exact form.
Solution:
- Complete the Square:
Halve -8 to get -4.
(x - 4)² - (-4)² + 5
(x - 4)² - 16 + 5
(x - 4)² - 11. (Here, a = -4, b = -11). - Solve:
(x - 4)² - 11 = 0
(x - 4)² = 11 - Square root both sides (remember ±):
x - 4 = ±√11 - Add 4:
x = 4 ± √11.
Answer: x = 4 + √11 or x = 4 - √11.
Real-World Application (Global Context)
Quadratic equations model trajectory and motion under gravity. This is essential in physics and sports analytics.
Scenario: Projectile Motion
A ball is thrown into the air. Its height h (in meters) after t seconds is given by the formula:
h = 20t - 5t²
To find when the ball hits the ground, we set height h = 0 and solve the quadratic equation:
- 5t² - 20t = 0
- Factorise: 5t(t - 4) = 0
- Solutions: t = 0 (start) and t = 4 (landing).
Engineers use more complex versions of these equations (using the Formula) to calculate the precise landing spots of rockets or aircraft.
Exam Technique and Common Pitfalls
1. The Negative 'b' Trap
When using the Quadratic Formula, if b is negative (e.g., -5), then -b becomes positive (5).
Also, when squaring b inside the root, put it in brackets: (-5)² = 25. Many calculators give -25 if you type -5², which ruins the calculation.
2. "Exact Form" vs. "Decimals"
Check the question command:
• "Give exact solutions" or "surd form" → Use Completing the Square or stop the Formula at the surd stage.
• "3 Significant Figures" → Use the Formula and round at the very end.
3. Harder Completing the Square (a > 1)
For 2x² + 8x + 1, you must factorise the 2 out of the x terms first:
2(x² + 4x) + 1
Then complete the square inside the bracket: 2[(x+2)² - 4] + 1
Expand: 2(x+2)² - 8 + 1 = 2(x+2)² - 7.
Solving quadratics is a core skill. If you are aiming for Grade 9, mastering Grade 9 algebra like completing the square for hard coefficients is essential.
Summary Checklist and Next Steps
Checklist:
- [ ] I can solve quadratics by factorising simple expressions.
- [ ] I have memorized the Quadratic Formula and can use it for decimals.
- [ ] I can complete the square for expressions like x² + bx + c.
- [ ] I know how to interpret the discriminant (positive/zero/negative).
- [ ] (H) I can solve equations leaving answers in surd form (exact values).
Practice Resources
Mastering quadratic equations requires consistent practice. Use our dedicated worksheet to test your skills on factorising, using the quadratic formula, and completing the square.
Download Topic Worksheet: Quadratic Equations (Solving Methods)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
Now that you can solve quadratics, you will apply this skill to Topic 2.7 Inequalities, where you find the ranges of x for which a quadratic is positive or negative.