IGCSE Maths: Mastering Prime Factorization, HCF, and LCM

Understanding the structure of numbers—how they are built from primes and how they relate to each other through factors and multiples—is a fundamental concept in mathematics. In the Edexcel IGCSE 4MA1 Higher Tier syllabus, these skills are essential not only for direct questions but also as crucial prerequisites for algebra and fractions.

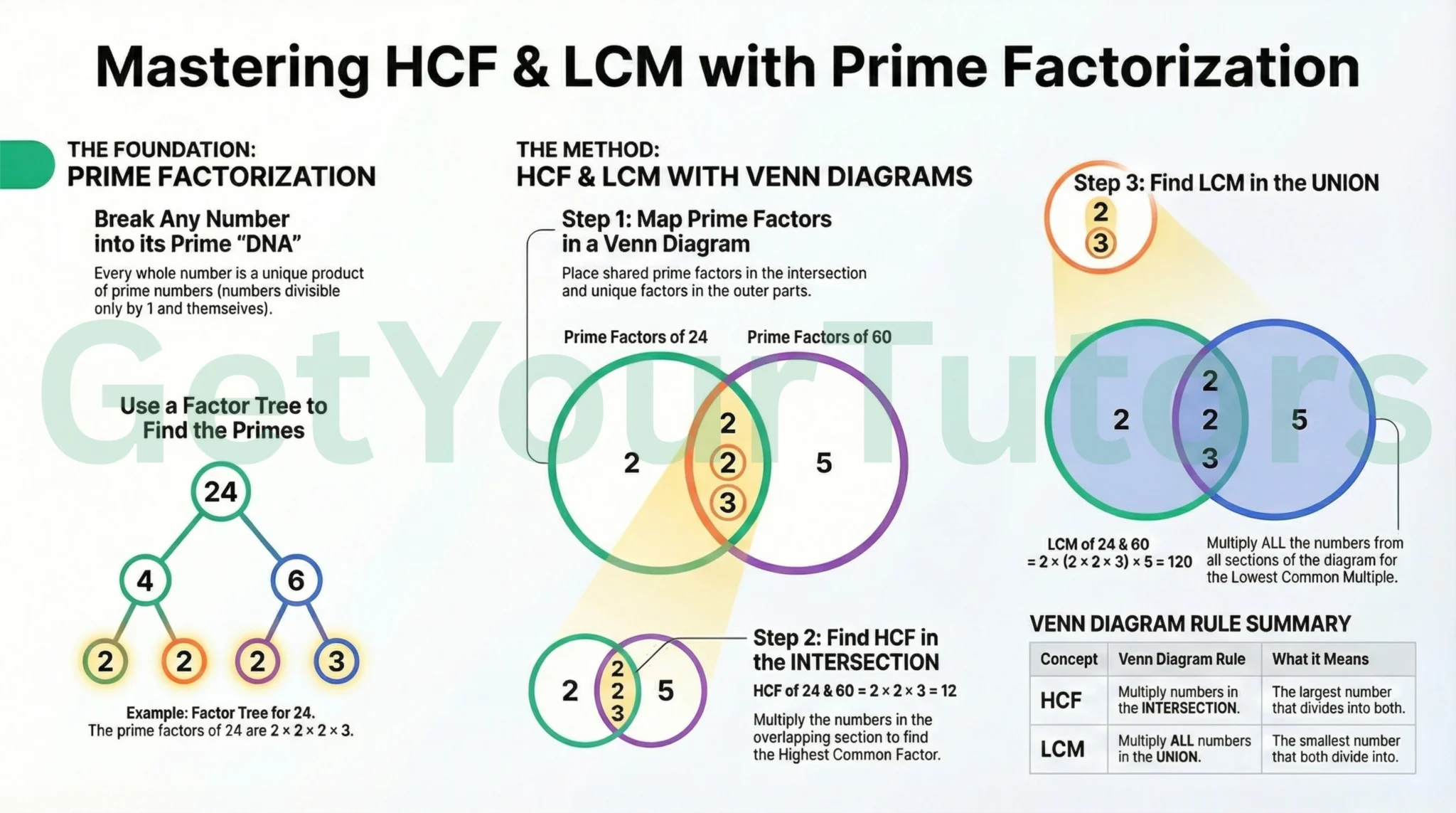
This guide provides a comprehensive overview of Topic 1.2 of the IGCSE Number System, focusing on the advanced techniques required to achieve Grades 7-9, including prime factorization and efficient methods for finding the Highest Common Factor (HCF) and Lowest Common Multiple (LCM).

Understanding Factors, Multiples, and Primes

Before diving into calculations, it is crucial to understand the core definitions.

Definitions (SGE Optimized)

• Factors: A factor of a number is an integer that divides the number exactly, leaving no remainder.
  • Example: The factors of 12 are 1, 2, 3, 4, 6, and 12.
• Multiples: A multiple of a number is the result of multiplying that number by an integer.
  • Example: The multiples of 12 are 12, 24, 36, 48, ...
• Prime Numbers: A prime number is a positive integer greater than 1 that has exactly two distinct factors: 1 and itself.
  • Example: 2, 3, 5, 7, 11, 13, ... (Note: 1 is not a prime number).

Prime Factorization (Product of Prime Factors)

The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be expressed as a unique product of prime numbers. This process is called prime factorization.

In IGCSE exams, you will often be asked to "Express [Number] as a product of its prime factors."

Method: The Factor Tree

1. Start with the number.
2. Split the number into any pair of factors.
3. If a factor is prime, circle it.
4. If a factor is composite (not prime), continue splitting it until all branches end in prime numbers.
5. Write the final answer using index notation (powers) for repeated factors.

Example: Express 180 as a product of its prime factors.

      180
     /   \
    18    10
   /  \   /  \
  2*   9 2*   5*
      / \
     3*  3*

Result: 180 = 2 × 2 × 3 × 3 × 5
Index Notation: 180 = 2² × 3² × 5

Highest Common Factor (HCF)

The Highest Common Factor (HCF) of two or more numbers is the largest integer that divides all of them exactly. HCF is crucial for simplifying expressions and algebraic factorization.

Method 1: Using Prime Factorization

This is the preferred method for the IGCSE Higher Tier, especially with large numbers.

1. Find the prime factorization of each number (in index notation).
2. Identify the prime factors that are common to all numbers.
3. For each common prime factor, select the lowest power present.
4. Multiply these lowest powers together to find the HCF.

Example: HCF of 180 and 168.
180 = 2² × 3² × 5
168 = 2³ × 3¹ × 7

Common primes: 2 and 3.
Lowest power of 2: 2²
Lowest power of 3: 3¹
HCF = 2² × 3 = 4 × 3 = 12.

Lowest Common Multiple (LCM)

The Lowest Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all of them. LCM is essential for finding common denominators when adding and subtracting fractions.

Method 1: Using Prime Factorization

1. Find the prime factorization of each number (in index notation).
2. Identify all unique prime factors present in any of the numbers.
3. For each unique prime factor, select the highest power present.
4. Multiply these highest powers together to find the LCM.

Example: LCM of 180 and 168.
180 = 2² × 3² × 5¹
168 = 2³ × 3¹ × 7¹

Unique primes: 2, 3, 5, 7.
Highest power of 2: 2³
Highest power of 3: 3²
Highest power of 5: 5¹
Highest power of 7: 7¹
LCM = 2³ × 3² × 5 × 7 = 8 × 9 × 5 × 7 = 2520.

The Venn Diagram Method (HCF and LCM Combined)

The Venn diagram method is a highly visual and efficient way to find both the HCF and LCM simultaneously, connecting this topic with Set Theory.

Steps:

1. Find the prime factorization of the numbers (A and B), listed out (not in index notation yet).
2. Draw a Venn diagram representing the sets of prime factors for A and B.
3. Place the common prime factors into the intersection.
4. Place the remaining prime factors into the appropriate segments.
5. HCF: The product of the factors in the intersection.
6. LCM: The product of all factors within the Venn diagram.

Example: HCF and LCM of 180 and 168.
180 = 2 × 2 × 3 × 3 × 5
168 = 2 × 2 × 2 × 3 × 7

Common factors: 2, 2, 3.

      180          168
    ( 3, 5 ) [ 2, 2, 3 ] ( 2, 7 )

HCF = 2 × 2 × 3 = 12.
LCM = 3 × 5 × (2 × 2 × 3) × 2 × 7 = 15 × 12 × 14 = 2520.

Video Lesson: Cracking the Code of HCF & LCM Word Problems

Step-by-Step Worked Examples

Real-World Application (Global Context)

The concepts of LCM are widely used in astronomy, engineering, and computer science for understanding cyclical phenomena and synchronization.

Scenario: Planetary Alignment

Imagine a star system with three planets orbiting a central star.
Planet A completes an orbit in 4 Earth years.
Planet B completes an orbit in 10 Earth years.
Planet C completes an orbit in 15 Earth years.

If all three planets are currently aligned in a straight line from the star, how many years will pass before they are all simultaneously aligned in the same position again?

Solution:

This is a synchronization problem requiring the Lowest Common Multiple (LCM) of the three orbital periods.

1. Prime Factorization of the periods:
   4 = 2²
   10 = 2 × 5
   15 = 3 × 5
2. Calculate LCM (Highest powers of all unique primes):
   Unique primes: 2, 3, 5.
   Highest powers: 2², 3¹, 5¹.
   LCM = 2² × 3 × 5 = 4 × 3 × 5 = 60.

Answer: The planets will align again in 60 Earth years.

Exam Technique and Common Pitfalls

Achieving top grades requires recognizing the intent of the question and avoiding common mistakes.

Confusing HCF and LCM Rules

• The biggest mistake: Students often confuse the rules when using prime factors.
• The Fix: Remember this counter-intuitive relationship: HCF (Highest) uses the lowest powers of common primes. LCM (Lowest) uses the highest powers of all primes.

Contextual Clues

Learn to identify whether a word problem requires HCF or LCM.

• HCF Questions: Keywords like "greatest possible distance," "largest groups," "dividing equally," or "sharing."
• LCM Questions: Keywords like "simultaneously," "next time together," "repeating events," or "alignment."

Index Notation Discipline

• When asked for the "product of prime factors," you must use index notation (e.g., 2³ × 3) rather than the expanded form (e.g., 2 × 2 × 2 × 3) or the calculated value (e.g., 24) to gain full marks (A1).

Showing Methodology (M1 Marks)

• Always show your factor trees or the list of prime factors clearly. This secures the Method mark (M1), even if the final calculation for HCF or LCM contains an arithmetic error. The prime factorization step is crucial.

Summary Checklist and Next Steps

You should now have a strong understanding of the relationships between numbers and the techniques required for the IGCSE exam.

Checklist:

• [ ] I can define and identify factors, multiples, and prime numbers.
• [ ] I can use factor trees to find the prime factorization of a number and express it using index notation.
• [ ] I can calculate the HCF using prime factors (lowest powers of common primes).
• [ ] I can calculate the LCM using prime factors (highest powers of all primes).
• [ ] I can use the Venn diagram method to find both HCF and LCM efficiently.
• [ ] I can solve advanced problems involving prime factors and unknown indices (Grade 9).
• [ ] I can identify whether a contextual problem requires the HCF or the LCM.

Next Steps:

The skills developed here are immediately applicable to the next topic: Topic 1.3 Fractions. Understanding LCM is vital for adding and subtracting fractions, while HCF is used for simplification.

For students aiming for Grades 8 and 9, mastering the complex problem-solving questions (like Example 4) is crucial. If you need help developing these advanced techniques, consider seeking personalized IGCSE Maths support.