The Ultimate Guide to the IGCSE Maths Number System (Edexcel 4MA1 Higher Tier)
The Number System is the bedrock of the Edexcel International GCSE (IGCSE) Mathematics A (4MA1) syllabus. While it accounts for approximately 22–28% of the total assessment weighting in the Higher Tier, its importance extends far beyond that. The skills developed in this section—accuracy, fluency, and logical reasoning—are essential tools used in every other area of the syllabus, including Algebra, Geometry, and Statistics.
This guide serves as your central hub for mastering Topic 1. We will explore the 11 key areas within the Number System, highlighting the advanced concepts required for the Higher Tier (H) to help students achieve Grades 7-9.
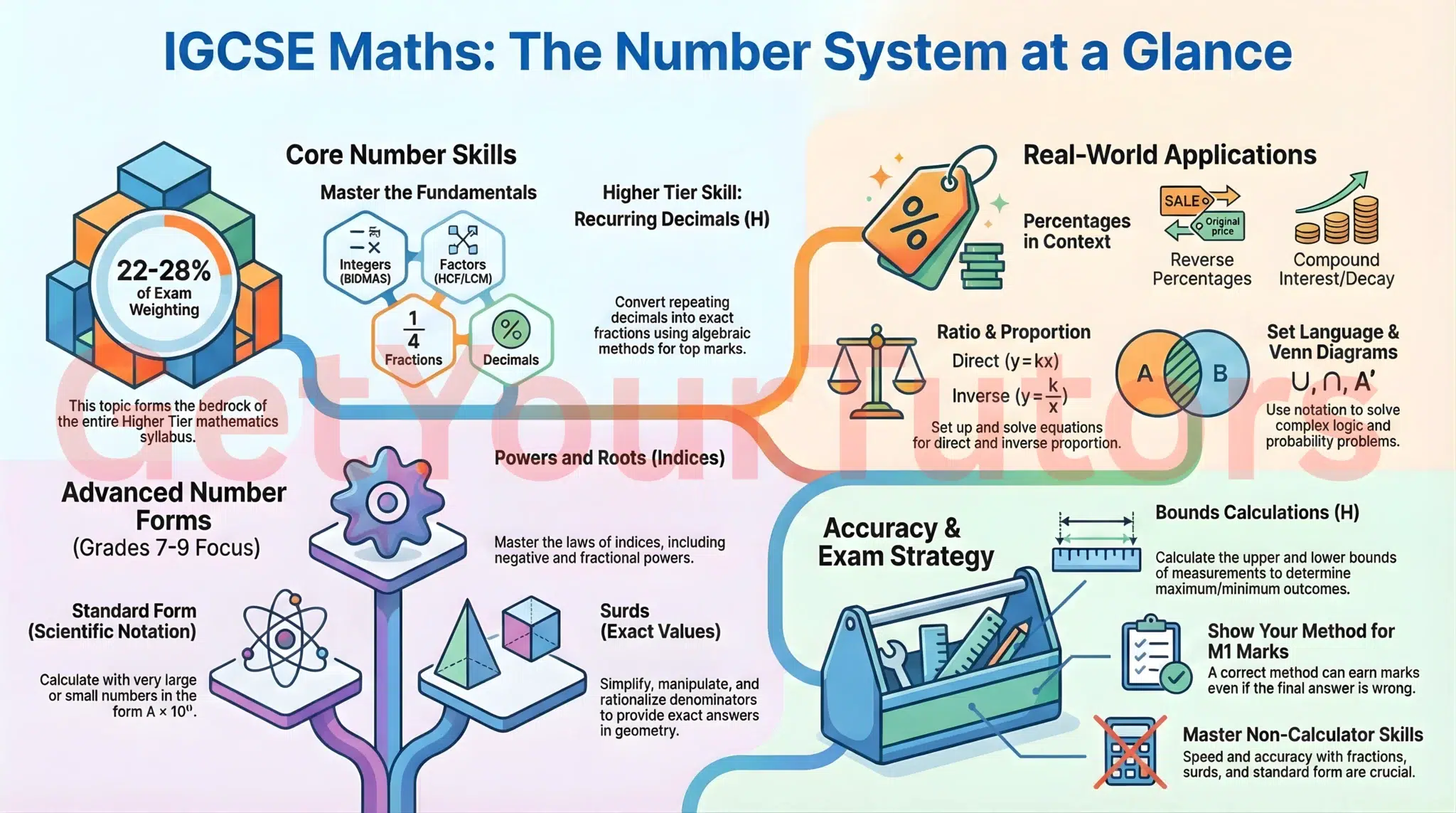
The Structure of the IGCSE Number System
The Edexcel 4MA1 specification requires a deep understanding of numerical operations, their applications, and the theoretical structure of numbers. We will explore these topics in four logical groups: Core Number Skills; Ratios, Percentages, and Proportion; Powers, Roots, and Forms; and Advanced Concepts.
Deep Dive: IGCSE Number Topics (4MA1 Higher Tier)
Below is a comprehensive overview of each sub-topic within the IGCSE Number System, organized thematically, with links to detailed revision guides.
Core Number Skills and Types (1.1 – 1.4, 1.6)
These topics form the essential toolkit for all mathematical calculations. Fluency and accuracy here are paramount.
1.1 Integers, BIDMAS, and Directed Numbers
This foundational topic ensures accuracy with whole numbers (integers) and negative numbers (directed numbers).
- Key Concepts: Rules for the four operations (+, -, ×, ÷) with negative numbers.
- BIDMAS/BODMAS: The strict conventional order of operations (Brackets, Indices, Division/Multiplication, Addition/Subtraction).
1.2 Factors, Multiples, and Prime Factorization
Understanding how numbers are constructed is vital for algebraic factorization and working with fractions.
- Key Concepts: Identifying factors and multiples.
- Prime Factorization: Expressing a number as a product of its prime factors.
- HCF and LCM: Calculating the Highest Common Factor and Lowest Common Multiple, often using prime factorization.
1.3 Fractions
Higher Tier students must be proficient in complex operations with fractions, often without a calculator.
- Key Concepts: Equivalency, simplifying, and ordering fractions.
- The four operations with fractions and mixed numbers.
1.4 Decimals and Conversions (H)
This involves the relationship between fractions and decimals.
- Key Concepts: Ordering decimals and conversions.
- Higher Tier (H): Recurring Decimals: Converting recurring decimals (e.g., 0.1̇8̇) into exact fractions using algebraic proof methods. This is a standard Grade 8/9 skill.
Powers, Roots, and Forms (1.5, 1.10, 1.11)
This section deals with how we represent numbers, from very large and small numbers to irrational numbers. These are crucial topics for Grades 7-9.
1.5 Powers and Roots (Indices) (H)
Indices (powers) provide a shorthand for repeated multiplication and are fundamental to algebra.
- Key Concepts: Squares, cubes, and roots. Laws of Indices (multiplication, division, powers of powers).
- Higher Tier (H): Negative Indices: Understanding reciprocals (a-n = 1/an).
- Higher Tier (H): Fractional Indices: Understanding roots (am/n = (n√a)m).
1.6 Set Language and Venn Diagrams
Set theory provides a precise language for classifying and organizing groups, bridging the gap between Number and Probability.
- Key Concepts: Understanding notation: Union (∪), Intersection (∩), Complement (A’), Universal Set (ℰ), and Empty Set (∅). Using Venn diagrams to solve categorization and logic problems.
Ratios, Percentages, and Proportion (1.7, 1.8)
These concepts are crucial for comparison, finance, and modeling relationships between quantities.
1.7 Percentages (H)
Percentages are essential for real-world mathematics and financial applications.
- Key Concepts: Conversions and calculating percentage change (profit/loss).
- Higher Tier (H): Reverse Percentages: Finding the original amount before a percentage change occurred.
- Higher Tier (H): Compound Interest, Growth, and Decay: Using multipliers to calculate repeated percentage changes.
1.8 Ratio and Proportion (H)
Ratios compare quantities, while proportion describes the relationship between changing variables.
- Key Concepts: Simplifying ratios and dividing an amount into a given ratio.
- Higher Tier (H): Direct Proportion (y=kx) and Inverse Proportion (y=k/x). This includes finding the constant of proportionality (k) and setting up equations.
1.9 Degree of Accuracy and Bounds (H)
All measurements are approximations. This topic deals with the implications of rounding and precision.
- Key Concepts: Rounding to significant figures (sf) and decimal places (dp). Estimation.
- Higher Tier (H): Upper and Lower Bounds: Calculating the maximum and minimum possible values of a measurement.
- Higher Tier (H): Bounds Calculations: Applying bounds to complex calculations (e.g., area, speed, density), including scenarios involving subtraction and division which require careful logical reasoning.
1.10 Standard Form
Standard Form (Scientific Notation) is a standardized way of writing very large or very small numbers.
- Key Concepts: Writing numbers in the form A × 10n, where 1 ≤ A < 10 and n is an integer. Performing the four operations in standard form, with or without a calculator.
1.11 Surds (H)
Surds are irrational roots (e.g., √5). Working with surds is essential for exact calculations in trigonometry and geometry.
- Higher Tier (H): Simplifying Surds: Reducing surds to their simplest form (e.g., √12 = 2√3).
- Higher Tier (H): Operations: Adding, subtracting, multiplying, and expanding brackets containing surds.
- Higher Tier (H): Rationalizing the Denominator: Removing the surd from the denominator of a fraction, including complex binomial denominators (e.g., 1/(3+√2)).
Advanced Concepts: Degree of Accuracy (1.9)
Synthesized Worked Example (Grade 9 Level)
The most challenging IGCSE questions often combine multiple areas of the number system. This example demonstrates how Bounds (1.9) and Standard Form (1.10) interact in a typical high-level problem.
Question:
A particle travels a distance D in time T.
D = 1.2 × 104 meters, correct to 2 significant figures.
T = 4.8 × 10-2 seconds, correct to 2 significant figures.
Calculate the lower bound for the speed of the particle. Give your answer in standard form to a suitable degree of accuracy.
Solution:
Step 1: Understand the formula for Speed.
Speed = Distance / Time (S = D/T).
Step 2: Determine how to calculate the Lower Bound for Speed (SLB).
To minimize the result of a division, we must use the smallest possible numerator and the largest possible denominator.
SLB = DLB ÷ TUB (Lower Bound of Distance / Upper Bound of Time).
Step 3: Calculate the required bounds for D and T.
For D = 1.2 × 104 m (12000 m):
The measurement is given to 2 significant figures. The degree of accuracy is the place value of the second significant figure (1000 m).
Half of this accuracy is 500 m.
Lower Bound (DLB) = 12000 - 500 = 11500 m.
For T = 4.8 × 10-2 s (0.048 s):
The degree of accuracy is the place value of the second significant figure (0.001 s).
Half of this accuracy is 0.0005 s.
Upper Bound (TUB) = 0.048 + 0.0005 = 0.0485 s.
Step 4: Perform the calculation.
SLB = 11500 ÷ 0.0485
SLB ≈ 237113.402... m/s.
Step 5: Convert the answer to Standard Form and round appropriately.
237113.402... = 2.37113402... × 105.
A suitable degree of accuracy usually matches the input data (2 or 3 significant figures).
Answer (to 3 sf): 2.37 × 105 m/s.
Exam Strategies for the IGCSE Number Section
Success in the Higher Tier exam relies on accuracy, efficiency, and clear methodology.
1. Master Non-Calculator Skills
A significant portion of the IGCSE assessment may be non-calculator. Students must be fluent and fast in mental arithmetic, operations with fractions, manipulating standard form, and simplifying surds without technological aid.
2. The Importance of Method Marks (M1)
Number questions often involve multiple steps. Always show your working clearly and logically.
- In Edexcel mark schemes, M1 denotes a mark awarded for the correct method.
- A1 denotes an accuracy mark for the final answer.
If you use the correct method (M1) but make a minor arithmetic error, you can still gain the majority of the marks if your methodology is clear (e.g., showing the bounds used in a calculation).
3. Contextual Interpretation and Formatting
Read the question carefully. Identify the required output (e.g., "Give your answer to 3 significant figures," "Leave your answer in standard form," or "Give an exact answer"—which implies using surds/fractions). Failing to adhere to the format can cost the final A1 mark.
4. Focus on Higher Tier Weak Spots
Ensure you dedicate sufficient revision time to the topics exclusive to the Higher Tier (Surds, Bounds Calculations, Fractional/Negative Indices, Recurring Decimals), as these are often the differentiators for Grades 7-9.
Summary and Next Steps
Mastering the IGCSE Number System is your first critical step toward achieving a top grade in the 4MA1 Higher Tier exam. It requires precision, a deep understanding of the underlying rules, and the ability to apply these concepts to sophisticated, synthesized problems.
Use this hub to navigate through each sub-topic, ensuring you have covered the detailed content in the linked guides.
Practice with IGCSE Maths Worksheets
Testing your knowledge is crucial for achieving Grades 7-9. Consolidate your learning with our comprehensive library of topic-specific worksheets and model answers.
Get Free IGCSE Edexcel Maths Worksheets & Answers
What's Next?
The next logical step in your revision journey is Topic 2: Equations, Formulae, and Identities, where you will apply these number skills in an algebraic context.
If you are aiming for Grades 8 or 9, ensuring complete mastery of these foundational topics is essential. Consider joining a comprehensive IGCSE Maths revision program to access expert guidance, targeted practice, and personalized feedback.