IGCSE Maths: Mastering the Laws of Indices, Negative, and Fractional Powers (H)
The Laws of Indices (also known as Powers and Roots) are fundamental rules governing how numbers and algebraic terms interact through multiplication and division. Mastery of these laws is critical for the Edexcel IGCSE 4MA1 Higher Tier syllabus, forming the backbone of algebra, calculus, and topics like Standard Form.
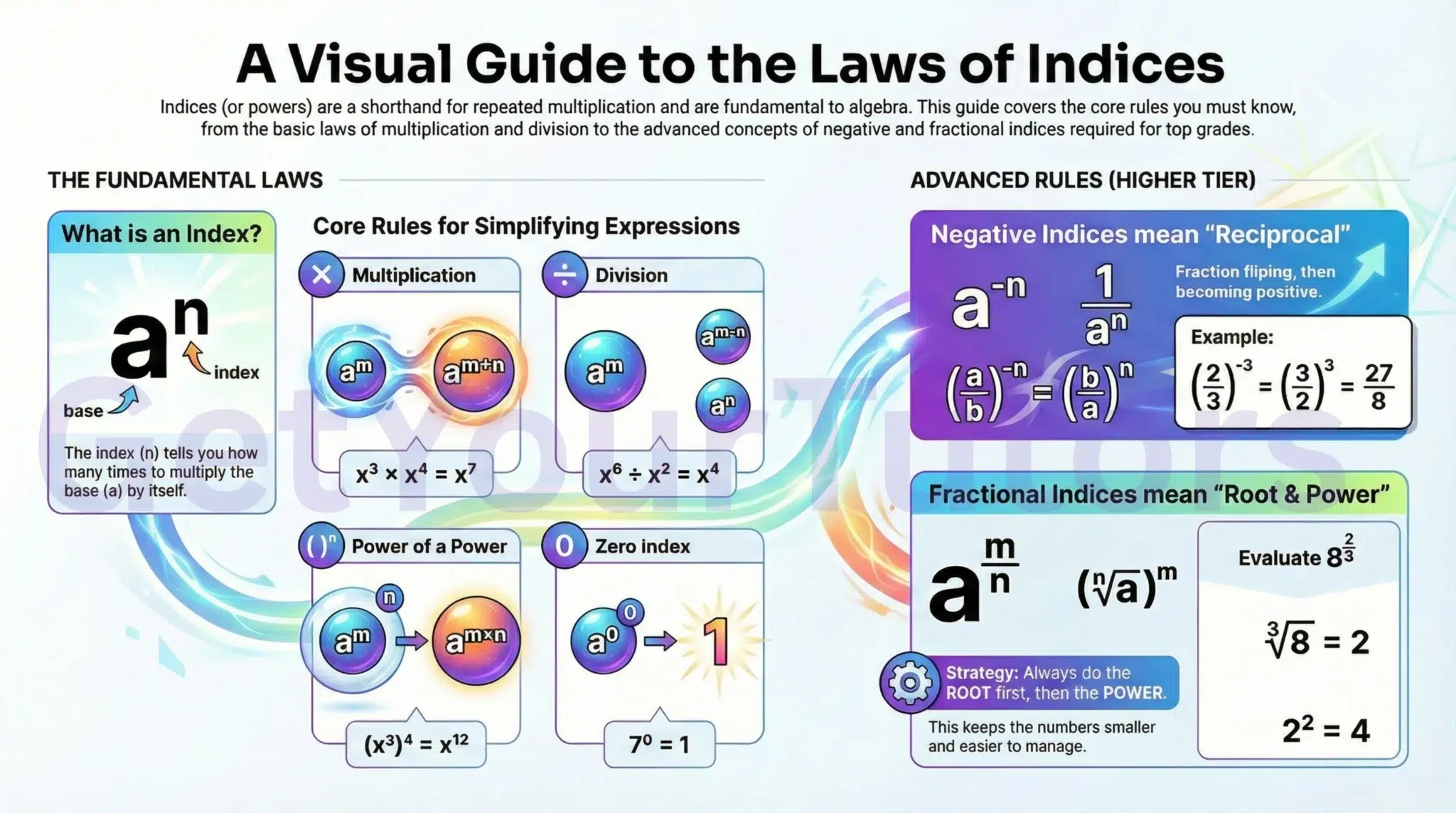
This guide provides a comprehensive overview of Topic 1.5 within the IGCSE Number System, focusing on the rigorous application of the core laws, and the advanced concepts of negative and fractional indices required for Grades 7-9.
Understanding Powers and Roots
Index notation is a shorthand for repeated multiplication.
In the expression an:
- a is the Base (the number being multiplied).
- n is the Index (or Power/Exponent) (how many times the base is multiplied by itself).
Example: 25 = 2 × 2 × 2 × 2 × 2 = 32.
Roots are the inverse operation of powers. The nth root of a number b (n√b) is the value a such that an = b.
- Square Root: √36 = 6.
- Cube Root: ∛8 = 2. (Using ∛ symbol for cube root)
The Fundamental Laws of Indices
The following laws must be memorized and applied fluently. These rules apply when the base is the same.
| Rule | Algebraic Form | Description | Example |
|---|---|---|---|
| 1. Multiplication | am × an = am+n | When multiplying, add the indices. | x3 × x4 = x7 |
| 2. Division | am ÷ an = am-n | When dividing, subtract the indices. | x6 ÷ x2 = x4 |
| 3. Power of a Power | (am)n = am×n | When raising a power to another power, multiply the indices. | (x3)4 = x12 |
| 4. Zero Index | a0 = 1 (a≠0) | Anything (except 0) raised to the power of zero is 1. | 70 = 1 |
| 5. Power of a Product | (ab)n = anbn | Apply the index to each factor inside the bracket. | (3x)2 = 32x2 = 9x2 |
Advanced Indices: Negative and Fractional (H)
The Higher Tier specification requires a deep understanding of how negative and fractional indices function.
6. Negative Indices (Reciprocals) (H)
Rule: A negative index signifies the reciprocal of the base raised to the positive index. It means "1 divided by."
a-n = 1an
Example: 5-2 = 152 = 125.
Fractions with Negative Indices:
When a fraction is raised to a negative power, flip the fraction (find the reciprocal) and make the power positive.
(ab)-n = (ba)n
Example: (23)-3 = (32)3 = 3323 = 278.
7. Fractional Indices (Roots) (H)
Rule: A fractional index represents a root.
Unit Fractions (Numerator = 1): The denominator indicates the type of root.
a1n = n√a
Example: 1612 = √16 = 4; 2713 = ∛27 = 3.
General Fractions (Numerator ≠ 1): The numerator indicates the power, and the denominator indicates the root.
amn = (n√a)m or n√(am)
Methodology: When evaluating, it is almost always easier to calculate the root first (to make the number smaller), and then apply the power.
Example: Evaluate 823.
1. Root (Denominator 3): ∛8 = 2.
2. Power (Numerator 2): 22 = 4.
Result: 4.
Video Lesson: Visualizing Negative Indices & The "Root First" Strategy
Step-by-Step Worked Examples
The following examples demonstrate the application of these laws in IGCSE exam-style questions.
Example 1: Basic Simplification (Grade 6/7)
Question: Simplify (2a4)34a5.
Solution:
- Simplify the Numerator (Power of a Product and Power of a Power) (M1):
(2a4)3 = 23 × (a4)3 = 8a12. - Rewrite the expression:
8a124a5 - Perform the Division (Division Law):
Divide the coefficients: 8 ÷ 4 = 2.
Subtract the indices: a12 ÷ a5 = a12-5 = a7. - Combine: 2a7 (A1).
Example 2: Evaluating Negative Indices (Grade 7/8)
Question: Evaluate (214)-2.
Methodology: When dealing with mixed numbers and indices, convert to an improper fraction first.
Solution:
- Convert to Improper Fraction:
214 = 94. - Rewrite the expression:
(94)-2 - Apply Negative Index Rule (Flip the fraction, make power positive) (M1):
(49)2 - Apply Power Rule:
4292 = 1681 (A1).
Example 3: Evaluating Complex Fractional Indices (Grade 8/9)
Question: Evaluate 12543.
Solution:
- Apply Fractional Index Rule (Root first, then Power) (M1):
12543 = (∛125)4. - Calculate the Root (Denominator):
∛125 = 5. - Calculate the Power (Numerator):
54 = 625 (A1).
Example 4: Synthesis of Negative and Fractional Indices (Grade 9)
Question: Evaluate (827)-23.
Solution:
- Apply Negative Index Rule (Flip fraction, make power positive) (M1):
(278)23 - Apply Fractional Index Rule (Root first) (M1):
(∛278)2 - Calculate the Root:
∛27 = 3; ∛8 = 2.
(32)2 - Calculate the Power:
3222 = 94 (A1).
Example 5: Solving Equations with Indices (Grade 9)
Question: Solve the equation 42x+1 = 8x+3.
Methodology: To solve for an unknown index, the bases must be the same on both sides of the equation. We use knowledge of prime factorization to find a common base.
Solution:
- Identify a Common Base: Both 4 and 8 can be expressed as powers of 2.
4 = 22; 8 = 23. - Rewrite the equation using the common base (M1):
(22)2x+1 = (23)x+3 - Apply Power of a Power Law (Multiply indices) (M1):
22(2x+1) = 23(x+3)
24x+2 = 23x+9 - Equate the Indices: Since the bases are now the same, the indices must be equal.
4x+2 = 3x+9 - Solve the linear equation:
4x - 3x = 9 - 2
x = 7 (A1)
Real-World Application (Global Context)
Indices are fundamental in science, finance, and biology for modeling exponential growth and decay.
Scenario: Radioactive Decay (Half-Life)
The amount of a radioactive substance remaining after a certain time is modeled using indices. The half-life is the time it takes for half of the substance to decay.
Problem: A substance has a half-life of 5 years. If we start with 400g, how much remains after 20 years?
Solution:
The formula for the remaining amount (A) is A = I × (0.5)n, where I is the initial amount and n is the number of half-lives that have passed.
- Calculate the number of half-lives (n):
Total time = 20 years. Half-life = 5 years.
n = 20 ÷ 5 = 4 half-lives. - Apply the formula:
A = 400 × (0.5)4.
(Using fractions: (0.5) = (12)).
A = 400 × (12)4. - Evaluate the index:
(12)4 = 1424 = 116. - Calculate the final amount:
A = 400 × 116 = 25.
Answer: 25g of the substance remains.
Exam Technique and Common Pitfalls
Accuracy with indices requires careful attention to detail and a solid understanding of the rules.
The "Coefficient Trap"
The most common error in algebraic simplification occurs when raising a product to a power.
- Error: (3x2)3 = 3x6.
- Fix: Remember the power applies to the coefficient as well. (3x2)3 = 33 × (x2)3 = 27x6.
Confusing the Rules
Students often confuse the Multiplication Law (add indices) and the Power of a Power Law (multiply indices).
- a5 × a3 = a8 (Add).
- (a5)3 = a15 (Multiply).
Fractional Indices Strategy: Root First!
When evaluating complex fractional indices (e.g., 3235), always calculate the root first to keep the numbers manageable. (5√32)3 = 23 = 8. Calculating the power first (323) makes the calculation extremely difficult without a calculator.
Negative Bases and BIDMAS
Be extremely careful when dealing with negative bases. The presence or absence of brackets changes the meaning entirely.
- (-3)2 = (-3) × (-3) = 9. (The base is -3).
- -32 = -(3 × 3) = -9. (The base is 3; the negative is applied after the power due to BIDMAS).
Developing fluency with these rules is crucial for advanced algebraic manipulation skills required for Grades 8 and 9.
Summary Checklist and Next Steps
Mastery of the Laws of Indices is essential for success in the Higher Tier IGCSE, as these rules underpin many advanced topics.
Checklist:
- [ ] I understand the concepts of Base, Index, Power, and Root.
- [ ] I have memorized and can apply the fundamental laws: Multiplication, Division, and Power of a Power.
- [ ] I know the Zero Index rule (a0=1).
- [ ] I can correctly apply powers to products, ensuring coefficients are included.
- [ ] (H) I understand Negative Indices as reciprocals (a-n = 1an).
- [ ] (H) I understand Fractional Indices as roots and powers (amn = (n√a)m).
- [ ] (H) I can evaluate complex numerical expressions involving negative and fractional indices.
- [ ] (H) I can solve equations involving indices by finding a common base (Grade 9 skill).
Practice Resources
Reinforce your understanding of the laws of indices, including negative and fractional powers, with our targeted practice materials. Applying these rules to exam-style questions is key to mastering this topic.
Download Topic Worksheet: Laws of Indices & Negative/Fractional Powers
Need more practice? Access our complete library of topic-specific worksheets and answers here:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
The skills learned here are immediately applied in Topic 1.10 (Standard Form) and Topic 1.11 (Surds), which relates closely to fractional indices. They are also fundamental to all subsequent Algebra topics (Section 2).
Perhaps the most crucial aspect of the MYP is the explicit focus on Approaches to Learning (ATL) skills. These are the transferable skills that underpin academic success and lifelong learning, and they are essential for the independent learning required in the DP.
The MYP focuses on developing five categories of ATL skills:
- Thinking Skills: (Critical thinking, creativity, reflection, transfer).
- Communication Skills: (Reading, writing, listening, speaking, presenting).
- Social Skills (Collaboration): (Teamwork, leadership, conflict resolution).
- Self-Management Skills: (Organization, time management, resilience, self-motivation).
- Research Skills: (Information literacy, media literacy, finding and citing sources).
Mastering these ATL skills during the MYP is the single best preparation for the demands of the IB Diploma.