IGCSE Maths: Mastering Integers, BIDMAS, and Directed Numbers
Welcome to the foundation of mathematics. Understanding integers, the correct order of operations (BIDMAS), and how to handle directed (negative) numbers is essential for success in the Edexcel International GCSE (IGCSE) Mathematics A (4MA1) Higher Tier exam.
While these concepts might seem basic, they are applied in almost every other topic. A single error with a negative sign or calculation sequence can cost crucial marks in high-tariff (Grade 8/9) questions. This guide provides a comprehensive overview of Topic 1.1, ensuring you have the accuracy required across the entire IGCSE Number System.
Understanding the Core Concepts
This section covers the fundamental definitions and rules required by the 4MA1 specification.
Integers and Directed Numbers
Integers are whole numbers. They can be positive (1, 2, 3, ...), negative (-1, -2, -3, ...), or zero (0). Fractions and decimals (e.g., 0.5 or 1/3) are not integers.
Directed numbers are numbers that possess both magnitude (size) and direction (positive or negative). They are essential for representing real-world concepts such as temperature below freezing, financial debt, or elevation below sea level.
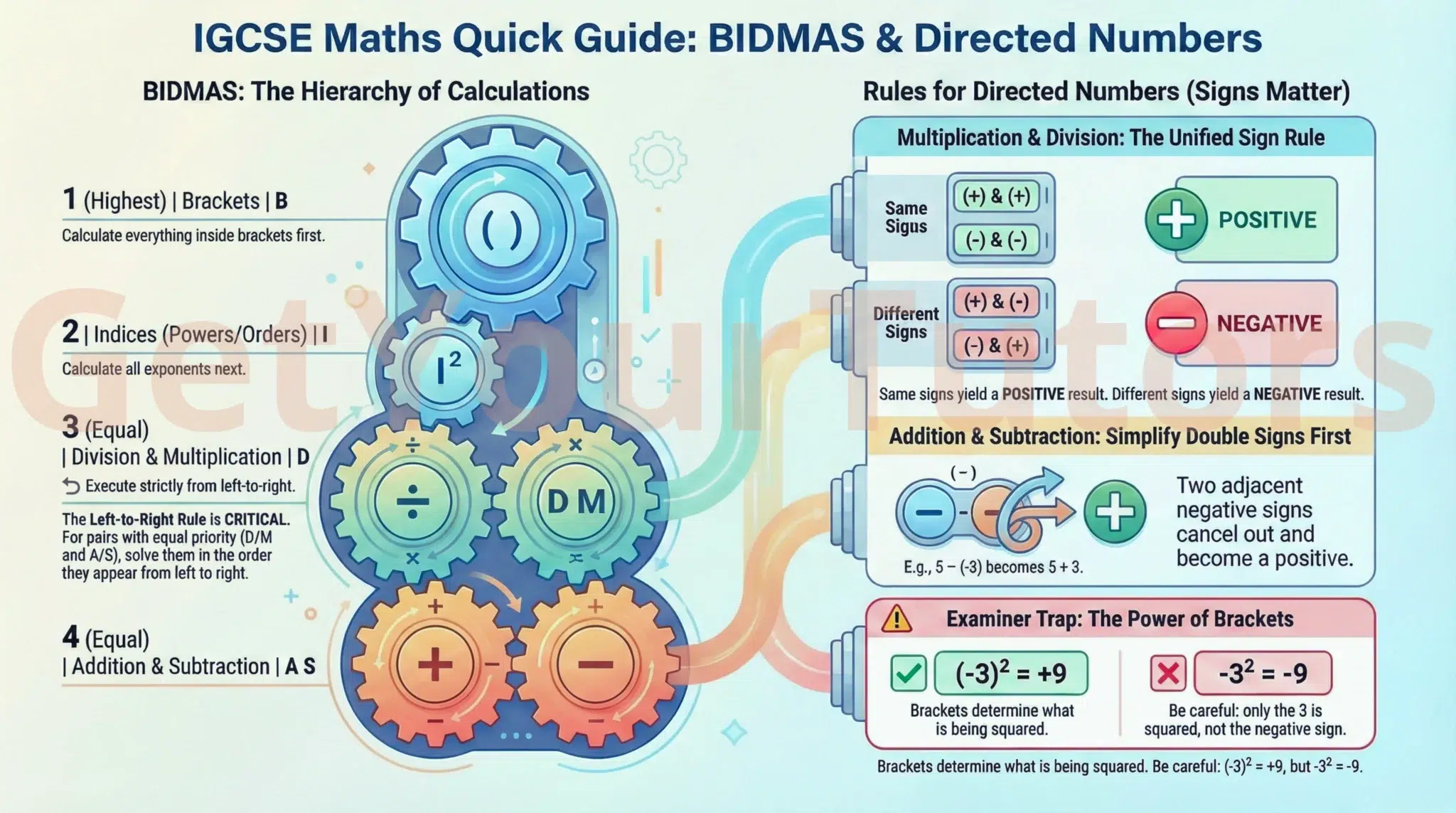
BIDMAS: The Order of Operations
When an expression contains multiple operations, the order in which they are performed matters significantly. BIDMAS (sometimes called BODMAS or PEMDAS) is the universal convention that defines this order.
The order is strictly as follows:
- B - Brackets: Calculate anything inside brackets first. If there are nested brackets, work from the inside out.
- I - Indices: Calculate Indices (powers and roots) (e.g., $5^2$ or $\sqrt{49}$).
- D & M - Division and Multiplication: These operations have equal priority.
- A & S - Addition and Subtraction: These operations also have equal priority.
It is crucial to remember that Division and Multiplication are equally important. When an expression contains both, you must work from left to right. The same applies to Addition and Subtraction.
Example: $20 \div 5 \times 2$.
Work left to right: $(20 \div 5) = 4$. Then $4 \times 2 = 8$.
Incorrect: Doing the multiplication first $(5 \times 2 = 10)$ and then $20 \div 10 = 2$.
Key Rules for Directed Numbers
The rules governing operations with negative numbers must be memorized and applied flawlessly.
Rules for Addition and Subtraction
The most crucial rule for calculations is the "Two Signs Together" Rule. This applies when two operational signs are next to each other in an expression:
- Adding a Negative (+ -): This is the same as subtraction.
Example: $7 + (-4)$ becomes $7 - 4 = 3$. - Subtracting a Negative (- -): This is the "double negative" rule, and it is the same as addition.
Example: $8 - (-2)$ becomes $8 + 2 = 10$.
Rules for Multiplication and Division
The rules for multiplication and division depend entirely on the signs of the two numbers involved:
- Same Signs = Positive Result
- Positive $\times$ Positive = Positive
- Negative $\times$ Negative = Positive (e.g., $-3 \times -4 = 12$)
- Different Signs = Negative Result
- Positive $\times$ Negative = Negative
- Negative $\times$ Positive = Negative (e.g., $3 \times -4 = -12$)
The exact same rules apply to division. For example, $-12 \div -3 = 4$ (same signs), and $12 \div -3 = -4$ (different signs).
Video Lesson: Visualizing BIDMAS Rules & The "Negative Number" Trap
Step-by-Step Worked Examples
We will now apply these rules to typical IGCSE-style questions of increasing difficulty.
Question: Evaluate $-8 + 5 \times (2 - 7)$.
Solution:
- B (Brackets): Calculate the value inside the brackets.
$(2 - 7) = -5$ - Rewrite the expression:
$-8 + 5 \times (-5)$ - M (Multiplication): Perform the multiplication before the addition.
$5 \times (-5) = -25$ (Different signs give a negative result). - Rewrite the expression:
$-8 + (-25)$ - A (Addition): Apply the rule for adding a negative (same as subtraction).
$-8 - 25 = -33$
Answer: -33
Question: Calculate the value of $\frac{(-4+6\times2)}{(10-3^{2}-5)}$.
Methodology: When dealing with complex fractions, treat the numerator (top) and the denominator (bottom) as if they are each enclosed in invisible brackets. Calculate them separately before performing the final division.
Solution:
- Analyze the Numerator: $(-4 + 6 \times 2)$
Apply BIDMAS (Multiplication first): $6 \times 2 = 12$
Complete Numerator (Addition): $-4 + 12 = 8$ - Analyze the Denominator: $(10 - 3^{2} - 5)$
Apply BIDMAS (Indices first): $3^{2} = 9$
Rewrite Denominator: $10 - 9 - 5$ - Complete Denominator (Subtraction, left to right):
$10 - 9 = 1$
$1 - 5 = -4$ - Final Calculation (Division): Numerator $\div$ Denominator
$8 \div (-4) = -2$ (Different signs give a negative result).
Answer: -2
Question: Given the expression $b^{2}-4ac$. Find the value of the expression when $a=2$, $b=-6$, and $c=-1$.
Methodology: This expression is the discriminant from the quadratic formula. Accuracy with negative substitution is vital. Always place brackets around negative numbers when substituting them into an expression.
Solution:
- Substitute the values:
$(-6)^{2} - 4(2)(-1)$ - I (Indices): Calculate the power.
$(-6)^{2} = (-6) \times (-6) = 36$ - Rewrite the expression:
$36 - 4(2)(-1)$ - M (Multiplication): Perform the multiplication.
$4(2)(-1) = 8(-1) = -8$ - Rewrite the expression: Be careful to keep the subtraction sign from the original formula.
$36 - (-8)$ - S (Subtraction): Apply the double negative rule (Subtracting a negative is the same as adding a positive).
$36 + 8 = 44$
Answer: 44
Real-World Application (Global Context)
Directed numbers and the order of operations are fundamental to fields like physics and engineering, allowing us to model situations involving movement and position relative to a reference point.
A research submarine is exploring an ocean trench. We use directed numbers to represent its elevation relative to sea level (0 meters).
- The submarine starts at an initial depth of -50 meters.
- It descends at a rate of 15 meters per minute for 10 minutes.
- It then ascends 45 meters.
- Finally, it descends another 80 meters to reach the observation point.
Problem: Calculate the final elevation of the observation point.
Solution:
We can represent this as a mathematical expression, using negative integers for descent and positive integers for ascent.
Initial Depth + (Descent Rate $\times$ Time) + Ascent Movement + Final Descent
$(-50) + (-15 \times 10) + 45 + (-80)$
We must apply BIDMAS to calculate the final position.
- M (Multiplication): Calculate the movement during the timed descent.
$-15 \times 10 = -150$ meters. - Rewrite the expression:
$(-50) + (-150) + 45 + (-80)$ - A (Addition/Subtraction): Work from left to right.
$(-50) + (-150) = -200$
$-200 + 45 = -155$
$-155 + (-80) = -155 - 80 = -235$
Answer: The final elevation of the observation point is -235 meters (235 meters below sea level).
Exam Technique and Common Pitfalls
Achieving Grades 7-9 requires not just knowing the rules, but applying them with strict discipline.
The Critical Error: Substitution and Indices
The most common high-level error involves squaring negative numbers during substitution. Edexcel examiners frequently test this distinction.
- The Rule: When substituting a negative number into any formula, always place the number in brackets.
- Correct Example: If $x = -4$, then $x^2 = (-4)^2 = 16$.
- Incorrect Example: Writing $-4^2$. According to BIDMAS, indices are calculated before the negative sign (which acts like multiplication by -1). Therefore, $-4^2$ means $-(4^2) = -16$.
BIDMAS Discipline and Method Marks
- Do Not Rush: Never attempt to perform multiple steps simultaneously.
- Show Your Steps (M1 Marks): Clearly show the result of each stage of BIDMAS. In Edexcel mark schemes, 'M1' denotes a Method mark, and 'A1' denotes an Accuracy mark. Showing your methodology ensures you gain M1 marks even if you make a small arithmetic error in the final A1 calculation.
- Fractions: Remember the 'invisible brackets' rule for fractions—calculate the numerator and denominator entirely before dividing.
Relevant Command Words
- Evaluate: Find the numerical value of the expression.
- Work out / Calculate: Similar to evaluate, requiring a numerical answer.
Summary Checklist and Next Steps
By completing this guide, you should now be confident in these foundational skills.
Checklist:
- [ ] I can define integers (positive, negative, zero) and directed numbers.
- [ ] I can confidently apply the four operations (+, -, $\times$, $\div$) to directed numbers.
- [ ] I know the multiplication/division rules (Same signs = Positive; Different signs = Negative).
- [ ] I understand the "double negative" rule (Subtracting a negative = Addition).
- [ ] I can strictly apply the BIDMAS order of operations, respecting the left-to-right rule for equal priority operations.
- [ ] I use brackets when substituting negative integers to avoid errors with indices.
Next Steps:
Once comfortable with integers, these skills will be immediately applied when you move on to basic algebraic manipulation and expanding brackets.
If you are aiming for the highest grades and want to ensure complete accuracy, consider personalized support through expert IGCSE Maths tutoring.