IGCSE Function Notation: Composite, Inverse & Domain Guide
In higher-level mathematics, we move away from simple equations like y = 2x + 3 and adopt Function Notation, written as f(x) = 2x + 3. This notation is a powerful tool that allows us to describe complex relationships, combine multiple rules, and reverse processes.
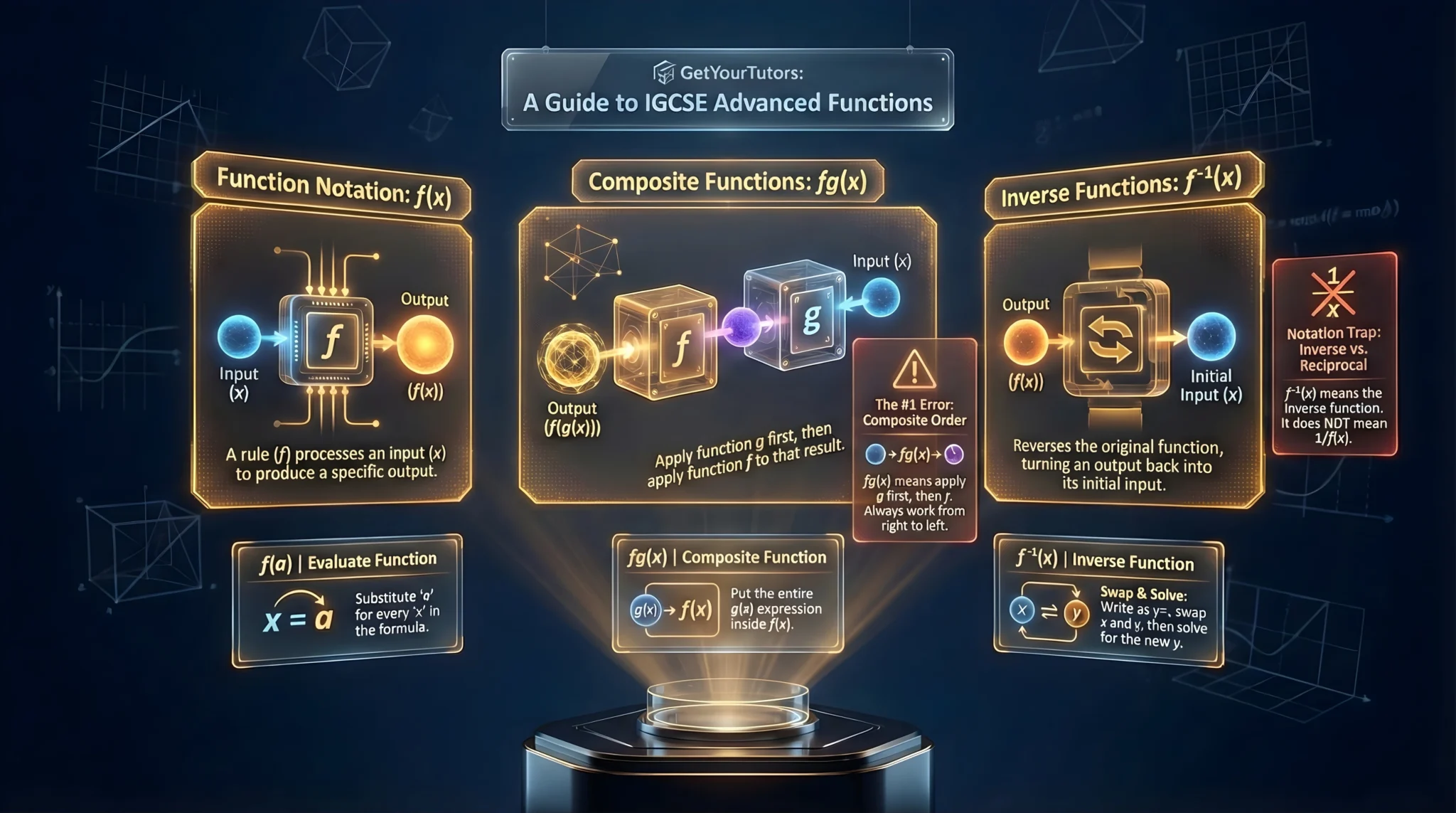
This guide covers Topic 3.2 of the IGCSE Functions & Graphs Hub. We will demystify the three pillars of Higher Tier functions: Evaluation, Composition (combining functions), and Inversion (undoing functions).
1. Understanding Function Notation
Think of a function, f, as a machine. It takes an input (x), applies a rule, and produces an output.
- f(x): Read as "f of x". It represents the output when the input is x.
- Evaluate f(5): Replace every x in the formula with 5.
Domain and Range (H)
You must be able to identify valid inputs and possible outputs.
- Domain: The set of all possible inputs (x-values).
Restricted Domain: You cannot divide by zero. For \(f(x) = \frac{1}{x-2}\), the domain is \(x \neq 2\). - Range: The set of all possible outputs (y-values).
Example: For \(f(x) = x^2\), the range is \(f(x) \geq 0\) (squares are always positive).
2. Composite Functions: fg(x) (H)
A composite function combines two functions. The notation fg(x) means "apply g first, then apply f to the result."
The Golden Rule: Inside-Out
Always work from the right to the left.
fg(x) means f( g(x) ).
1. Take the expression for g(x).
2. Put it INSIDE f(x).
3. Inverse Functions: f⁻¹(x) (H)
The inverse function reverses the operation of the original function. If f turns input A into output B, then f⁻¹ turns B back into A.
The "Swap and Solve" Method
- Write the function as y = ...
- Swap x and y (so y becomes x, and x becomes y).
- Rearrange the formula to make the new y the subject.
- Replace y with the notation f⁻¹(x).
Key Notation Summary
| Notation | Meaning | Action |
|---|---|---|
| f(a) | Evaluate | Substitute 'a' into the equation. |
| fg(x) | Composite | Put g(x) inside f(x). |
| f⁻¹(x) | Inverse | Swap x and y, then solve for y. |
Step-by-Step Worked Examples
Question: Given f(x) = x² + 1 and g(x) = 2x - 3, find the value of fg(4).
Methodology: Work inside out. Find g(4) first.
Solution:
- Find g(4):
g(4) = 2(4) - 3 = 8 - 3 = 5. - Apply f to the result:
fg(4) = f(5).
f(5) = 5² + 1 = 25 + 1 = 26.
Answer: 26.
Question: Given f(x) = 3x + 2 and g(x) = x², find an expression for gf(x) in its simplest form.
Methodology: We are putting the entire expression for f(x) into g(x).
Solution:
- Notation: gf(x) = g( f(x) ).
- Substitute: Replace the 'x' in g(x) with (3x + 2).
g(3x + 2) = (3x + 2)². - Expand (Algebraic Manipulation):
(3x + 2)(3x + 2) = 9x² + 6x + 6x + 4.
Answer: 9x² + 12x + 4.
Question: Find the inverse function f⁻¹(x) for f(x) = 2x + 1x - 3.
Methodology: This is a classic Grade 9 question where x appears twice. Use the Swap & Rearrange method.
Solution:
- Write as y: y = 2x + 1x - 3
- Swap x and y: x = 2y + 1y - 3
- Rearrange for y:
- Multiply by (y - 3): x(y - 3) = 2y + 1
- Expand: xy - 3x = 2y + 1
- Collect y terms: xy - 2y = 3x + 1
- Factorise y: y(x - 2) = 3x + 1
- Divide: y = 3x + 1x - 2
Answer: f⁻¹(x) = 3x + 1x - 2.
Real-World Application (Global Context)
Functions are essential in computer programming, particularly in data security and conversion.
Scenario: Currency Conversion & Fees
Imagine an international payment system.
- Function c(x) converts USD ($) to Euros (€): c(x) = 0.9x.
- Function f(x) applies a €5 service fee: f(x) = x - 5.
The final amount a customer receives depends on the order.
fc(x) means convert first, then subtract fee: 0.9x - 5.
cf(x) means subtract fee first, then convert: 0.9(x - 5) = 0.9x - 4.5.
Banks use composite functions to ensure fees are applied in the correct order. To reverse a transaction (refund), they must calculate the inverse function.
Exam Technique and Common Pitfalls
1. The Order of Composite Functions
This is the most common error.
• fg(x) means g first, then f.
• gf(x) means f first, then g.
Think of it like reading "f of g of x".
2. Inverse Notation Confusion
Do not confuse f⁻¹(x) with indices.
• In algebra, x⁻¹ means 1x.
• In functions, f⁻¹(x) means the inverse function, not the reciprocal.
3. Domain Errors
When finding domains of rational functions like f(x) = 1/(x-5), always set the denominator to zero to find the excluded value. Here, x ≠ 5.
Mastering advanced function algebra is essential for securing Grade 9 marks, particularly in the final questions of the paper.
Summary Checklist and Next Steps
Checklist:
- [ ] I can evaluate a function by substituting a number (e.g., f(3)).
- [ ] I can find a composite function fg(x) by substituting g into f.
- [ ] I can find an inverse function f⁻¹(x) by swapping variables and rearranging.
- [ ] (H) I can identify restricted values in a domain (e.g., dividing by zero).
Practice Resources
Mastering composite and inverse functions requires algebraic precision. Use our dedicated worksheet to test your skills on finding inverses and evaluating complex composite functions.
Download Topic Worksheet: Function Notation, Composite & Inverse
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
Now that you understand function notation, you are ready to visualize these relationships. Topic 3.3 Linear Graphs explores the visual representation of f(x) = mx + c.