IGCSE Maths: The Complete Guide to Fractions and Mixed Numbers (Edexcel 4MA1)

Fluency with fractions is non-negotiable for success in the Edexcel IGCSE Mathematics A (4MA1) Higher Tier. While calculators can assist, many questions specifically require students to perform operations manually and "show all your working." Furthermore, the rules governing numerical fractions are the foundation for advanced topics, particularly Algebraic Fractions.

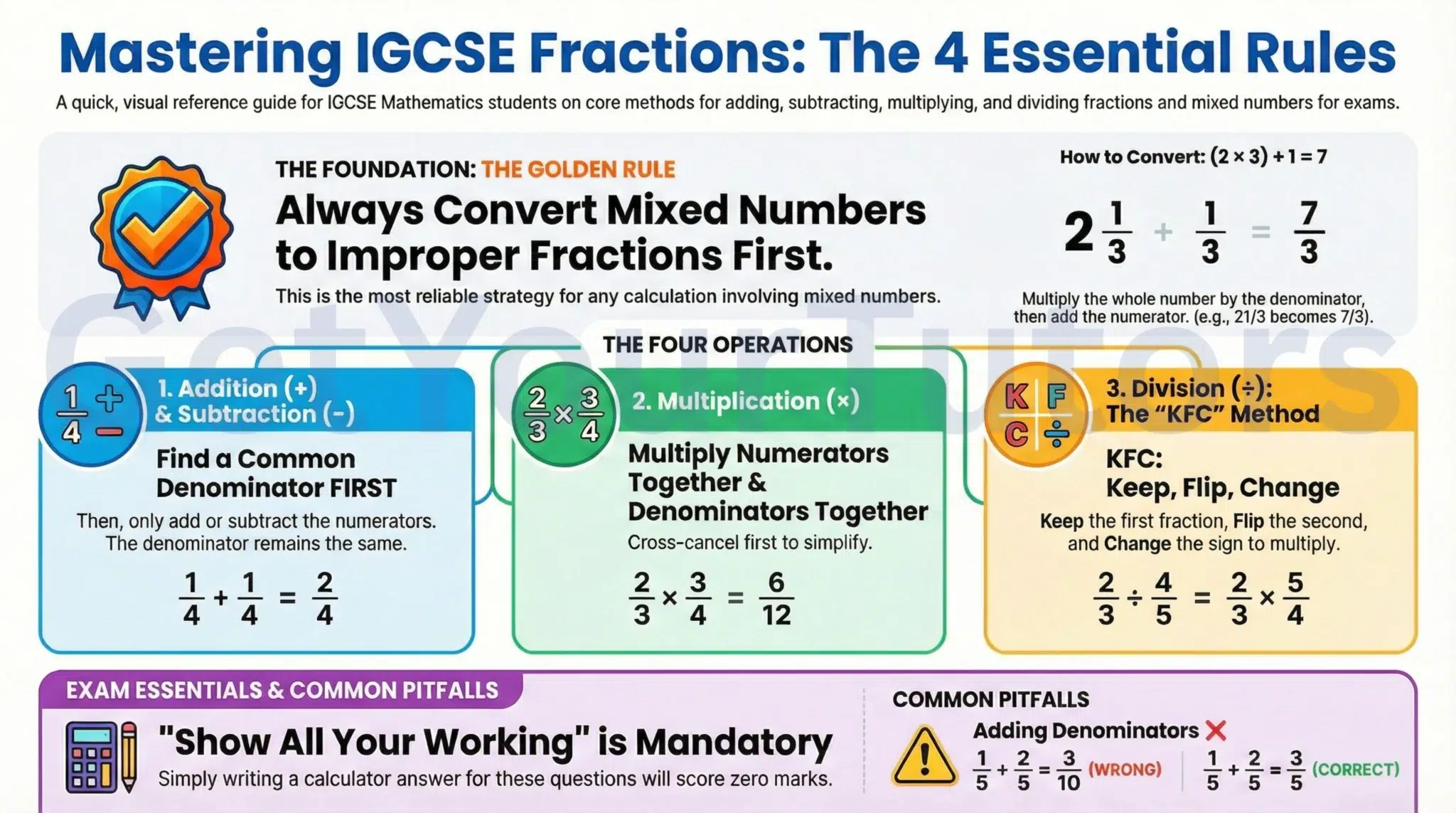
This guide provides a comprehensive overview of Topic 1.3 of the IGCSE Number System, detailing the four operations, handling mixed numbers, equivalency, and the rigorous techniques required to achieve Grades 7-9.

Understanding Fractions: Core Concepts

A fraction represents a part of a whole or a division of two integers.

Key Definitions

• Numerator: The top number (how many parts you have).
• Denominator: The bottom number (the total number of equal parts the whole is divided into).
• Proper Fraction: The numerator is smaller than the denominator (value < 1). E.g., 23.
• Improper Fraction (Top-heavy): The numerator is greater than or equal to the denominator (value ≥ 1). E.g., 73.
• Mixed Number: Consists of an integer part and a proper fraction part. E.g., 213.

Conversions

You must be able to convert fluently between mixed numbers and improper fractions. This is essential for calculations.

Mixed to Improper:
Multiply the whole number by the denominator, then add the numerator. This result becomes the new numerator; the denominator stays the same.
Example: 213 = (2×3)+13 = 73.

Improper to Mixed:
Divide the numerator by the denominator. The quotient (result of division) is the whole number part. The remainder becomes the numerator of the fraction part.
Example: 73. 7 ÷ 3 = 2 remainder 1. Result: 213.

Equivalency, Simplification, and Ordering

Simplification and Equivalency

Equivalent fractions have the same value (e.g., 12 = 510).

To simplify a fraction (write it in its simplest form), divide both the numerator and the denominator by their Highest Common Factor (HCF).

Ordering Fractions

To compare or order fractions, they must share a common denominator.

1. Find the Lowest Common Multiple (LCM) of the denominators. This is the Lowest Common Denominator (LCD).
2. Convert each fraction to an equivalent fraction using the LCD.
3. Compare the numerators.

Example: Which is larger, 56 or 79?
LCM of 6 and 9 is 18.
56 = 1518; 79 = 1418.
Since 15 > 14, 56 is larger.

The Four Rules of Fractions

Mastering the four operations (+, -, ×, ÷) is the core of this topic.

The Golden Rule for Mixed Numbers

When performing calculations with mixed numbers, the safest and most reliable strategy for IGCSE is to always convert them to improper fractions first.

Addition and Subtraction

Rule: You must have a common denominator before adding or subtracting.

Steps:

1. Convert mixed numbers to improper fractions.
2. Find the Lowest Common Denominator (LCD).
3. Write equivalent fractions using the LCD.
4. Add or subtract the numerators. The denominator remains the same.
5. Simplify the result.

Multiplication

Rule: No common denominator is needed. Multiply the numerators together and multiply the denominators together.

Steps:

1. Convert mixed numbers to improper fractions.
2. Cross-cancel (Highly Recommended): Look diagonally across the multiplication. If a numerator and a denominator share a common factor, divide them both by that factor. This simplifies the numbers before multiplication.
3. Multiply the (simplified) numerators and denominators.
4. Simplify the final result.

Division

Rule: To divide by a fraction, multiply by its reciprocal (the fraction flipped upside down).

Steps (The "KFC" Method):

1. Convert mixed numbers to improper fractions.
2. Keep the first fraction the same.
3. Flip the second fraction (the divisor).
4. Change the division sign (÷) to a multiplication sign (×).
5. Proceed using the rules for multiplication (including cross-canceling).

Video Lesson: The Ultimate IGCSE Fractions Toolkit & Exam Strategy

Step-by-Step Worked Examples

These examples demonstrate the rigorous methodology required for IGCSE exams, where showing all steps is often mandatory for Method Marks (M1).

Real-World Application (Global Context)

Fractions are critical in finance and economics, particularly when dealing with portfolio allocation and investment distribution.

Scenario: Portfolio Allocation

An investor is structuring their retirement fund. They allocate their capital as follows:

• 13 in Global Equities
• 14 in Bonds
• 16 in Real Estate

The remainder of the fund is held in Cash.

Problem: What fraction of the retirement fund is held in Cash?

Solution:

1. Find the total fraction already allocated:
   We need to calculate 13 + 14 + 16.
2. Find the LCD: The LCM of 3, 4, and 6 is 12.
3. Write Equivalent Fractions:
   412 + 312 + 212
4. Add Numerators:
   4+3+212 = 912.
5. Simplify the allocated fraction:
   912 = 34.
6. Calculate the remainder (Cash): The whole fund is represented by 1.
   1 - 34 = 44 - 34 = 14.

Answer: 14 of the fund is held in Cash.

Exam Technique and Common Pitfalls

Accuracy and methodology are paramount when dealing with fractions in the IGCSE exam.

The "Show All Your Working" Mandate

If an IGCSE question involves mixed numbers and asks you to "Show all your working," using a calculator to get the answer and writing it down will score zero marks. You must demonstrate the methodology (conversions, common denominators, KFC) to earn Method marks (M1).

Common Errors

1. Adding Denominators:
   • Error: 15 + 25 = 310.
   • Fix: The denominator stays the same: 35.
2. Errors with Mixed Number Multiplication:
   • Error: Students sometimes multiply the whole numbers and then multiply the fractions (e.g., 213 × 312 = 616). This is incorrect.
   • Fix: Always convert mixed numbers to improper fractions first.
3. Failing to Cross-Cancel: While not strictly an error, failing to cross-cancel makes the calculation significantly harder (e.g., 185 × 2512 = 45060) and increases the chance of arithmetic mistakes, especially when mastering non-calculator techniques.

Subtraction and "Borrowing"

While some students learn to subtract mixed numbers by "borrowing" from the whole number, this method is prone to errors. The improper fraction method is mathematically more robust and generally preferred for IGCSE.

Summary Checklist and Next Steps

Confidence with fractions is a powerful asset in the IGCSE exam. Ensure you can perform these operations accurately and efficiently.

Checklist:

• [ ] I can define and identify proper fractions, improper fractions, and mixed numbers.
• [ ] I can fluently convert between mixed numbers and improper fractions.
• [ ] I can simplify fractions and find equivalent fractions.
• [ ] I can order fractions by finding the Lowest Common Denominator (LCM/LCD).
• [ ] I can add and subtract fractions (including mixed numbers) using common denominators.
• [ ] I can multiply fractions, utilizing cross-cancelling for efficiency.
• [ ] I can divide fractions using the KFC method (multiplying by the reciprocal).
• [ ] I understand the importance of showing clear methodology for M1 marks.

Next Steps:

The immediate applications of these skills are in converting fractions to decimals (Topic 1.4) and percentages (Topic 1.7). For Higher Tier students, the most critical application is mastering Algebraic Fractions (Topic 2.2), which uses the exact same rules applied to algebraic expressions.