IGCSE Formulae: Substitution and Changing the Subject (H)
Formulae are the bridges between abstract algebra and the real world. Whether determining the speed of a car or the resistance of an electrical circuit, formulae allow us to calculate unknown values. In the Edexcel IGCSE 4MA1 Higher Tier exam, you must master two key skills: substituting values accurately (especially negatives) and rearranging complex formulae to change the subject.
This guide covers Topic 2.3 of the IGCSE Algebra Hub, taking you from basic substitution to Grade 9 rearranging problems where the subject appears twice or is trapped inside a root.
1. Substitution: The Foundation
Substitution involves replacing the variables (letters) in a formula with specific numbers to calculate a value.
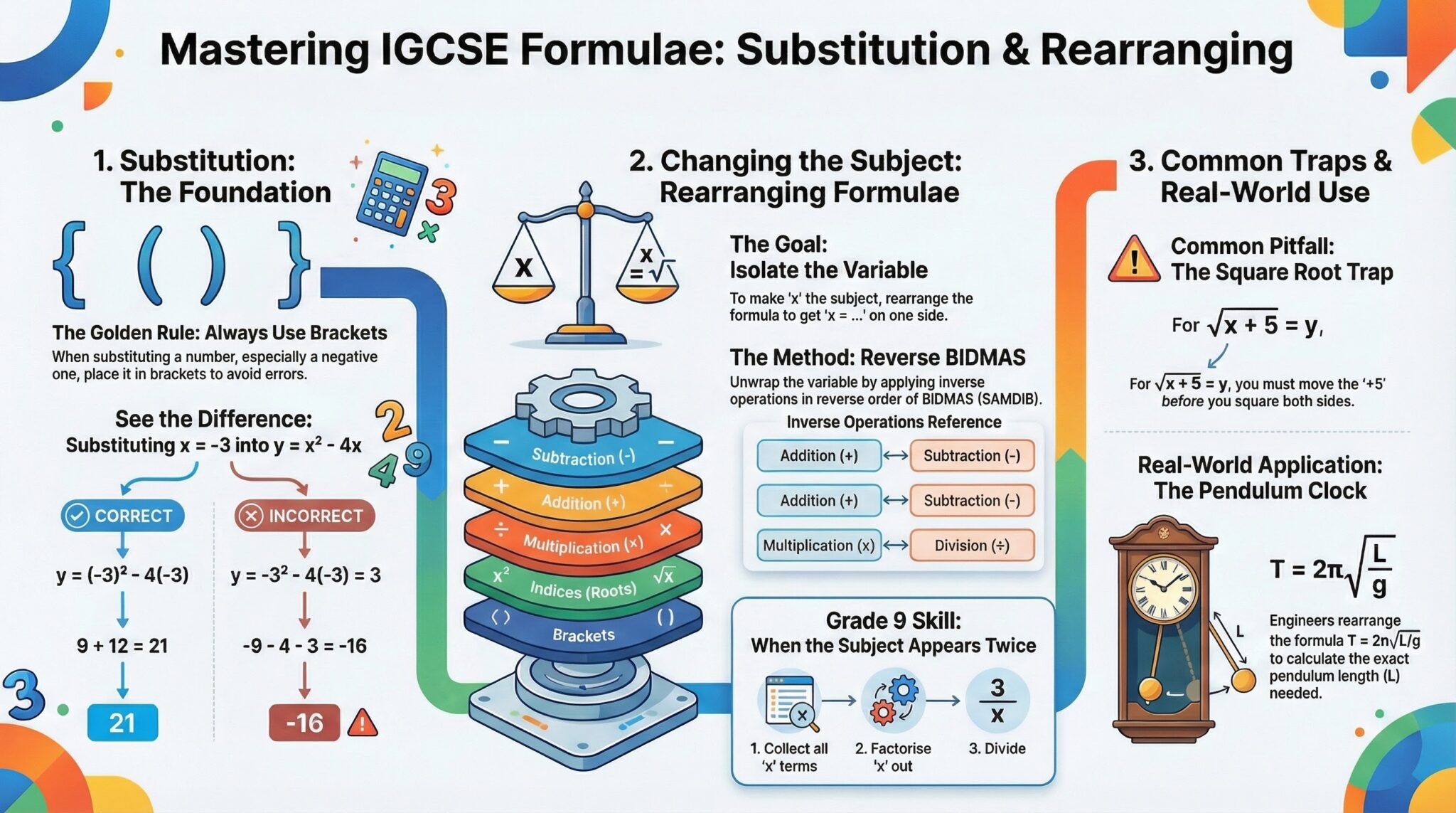
The "Golden Rule" of Substitution
When substituting a number, especially a negative number, always place it in brackets. This ensures you follow the correct BIDMAS and negative numbers rules.
- Formula: y = x² - 4x
- Substitute x = -3:
- Correct: y = (-3)² - 4(-3) = 9 + 12 = 21.
- Incorrect: y = -3² - 4 - 3 = -9 - 7 = -16. (Calculator error: squaring only the 3, not the negative).
2. Rearranging Formulae (Changing the Subject)
To "make x the subject" means to manipulate the formula until you have x = ... on one side, with no x terms on the other side.
The Balance Method (Reverse BIDMAS)
To isolate a variable, you generally perform operations in the reverse order of BIDMAS (SAMDIB). Unwrap the layers surrounding the subject.
Complex Cases (Higher Tier)
For Grades 7-9, you will encounter three specific challenges:
- Roots and Powers: To remove a square root, square both sides. To remove a square, take the square root.
- Fractions: Always multiply to remove fractions as your first step.
- Subject Appears Twice: If the subject (e.g., x) appears on both sides or in the top and bottom of a fraction, you must collect terms and factorise.
Key Formulas & Operations
Memorize the inverse operations required to "unwrap" a variable.
| Operation | Inverse Operation |
|---|---|
| Addition (+) | Subtraction (-) |
| Multiplication (×) | Division (÷) |
| Square (x²) | Square Root (√x) |
| Nth Power (xⁿ) | Nth Root (ⁿ√x) |
| Reciprocal (1/x) | Reciprocal (1/y) (Flip both sides) |
Step-by-Step Worked Examples
Question: Use the formula v = u + at to find v when u = 15, a = -9.8, and t = 4.
Solution:
- Substitute with brackets: v = (15) + (-9.8)(4).
- Multiply first (BIDMAS): v = 15 + (-39.2).
- Add/Subtract: v = 15 - 39.2 = -24.2.
Answer: v = -24.2.
Question: Make r the subject of the formula: A = 4πr².
Methodology: Reverse BIDMAS. Remove the multiply by 4π first, then the power.
Solution:
- Divide by 4π: A4π = r².
- Square root both sides: A4π = r.
- (Since r represents a length, we assume the positive root).
- Simplifying the root (Optional but good practice): r = √(A4π) = √A2√π.
Answer: r = √(A4π).
Question: Make x the subject of the formula: y = 3x + 5x - 2.
Methodology: The subject x is on top and bottom. Use the "Collect → Factorise → Divide" algorithm.
Solution:
- Multiply by the denominator (x - 2):
y(x - 2) = 3x + 5 - Expand the brackets:
xy - 2y = 3x + 5 - Collect all x terms on one side, non-x terms on the other:
xy - 3x = 5 + 2y - Factorise x out of the LHS (This is the crucial step):
x(y - 3) = 5 + 2y - Divide by the bracket (y - 3):
x = 5 + 2yy - 3
Answer: x = 2y + 5y - 3.
Real-World Application (Global Context)
Rearranging formulae is a daily task for physicists and engineers.
Scenario: The Simple Pendulum
The time period (T) of a swinging pendulum is given by the formula:
T = 2π√(Lg)
Where L is the length of the string and g is gravity. If an engineer wants to build a clock that ticks exactly once every second (T=1), they cannot simply plug numbers in. They must rearrange the formula to find the required Length (L).
- Divide by 2π: T2π = √(Lg).
- Square both sides: (T2π)² = Lg.
- Multiply by g: L = g(T2π)².
This rearranged formula allows the engineer to calculate the exact length needed for any time period.
Video Masterclass: Visualizing the 'Subject Appears Twice' & Engineer's Puzzle
Exam Technique and Common Pitfalls
1. The "Square Root" Trap
When moving a term like +5 away from a square root, you must move the 5 before squaring.
- Given: √x + 5 = y
- Incorrect: x + 25 = y² (Squaring individual terms).
- Correct: √x = y - 5 → x = (y - 5)².
2. Factorising is Key
If you end up with x = 5 + 2y - xy, you have not finished. The subject (x) is still on the right-hand side. You must group the x terms and factorise (as shown in Example 3).
3. Checking Your Answer
You can check algebraic rearrangement by using simple numbers.
In Example 3, if x=3, then y = (9+5)/(3-2) = 14.
Test your answer: x = (2(14)+5)/(14-3) = 33/11 = 3. It works!
If you want to ensure you can handle these high-tariff questions, mastering high-tariff algebraic questions is the best way to secure the top grades.
Summary Checklist and Next Steps
Checklist:
- [ ] I can substitute positive and negative numbers into formulae (using brackets).
- [ ] I can rearrange simple linear formulae (Reverse BIDMAS).
- [ ] I can rearrange formulae involving squares and roots.
- [ ] (H) I can rearrange formulae where the subject appears on both sides (Collect & Factorise).
- [ ] (H) I can check my rearrangement using substitution.
Practice Resources
Mastering the skill of changing the subject requires practice, especially with complex algebraic fractions. Use our dedicated worksheet to test your ability to rearrange formulae efficiently.
Download Topic Worksheet: Formulae, Substitution & Rearranging
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
Now that you can manipulate variables, you are ready to solve for them. The next topic is Topic 2.4 Linear Equations, where we find the specific value of an unknown.