Decimals& Recurring Fractions.

What are the types of decimals?

In IGCSE Maths, decimals fall into three categories. Understanding each type is essential for the Higher tier, where you must classify and convert between them.

• Terminating decimals — these have a finite number of decimal places and stop. For example, 0.375 and 0.8 are terminating. They are always rational because they can be written as fractions (0.375 = 3/8).
• Recurring decimals — these have one or more digits that repeat in an endless cycle. For example, 0.333... (written 0.3 with a dot above the 3) and 0.142857142857... are recurring. They are also rational because the algebraic method converts them to fractions.
• Irrational decimals — these go on forever with no repeating pattern. Examples include pi and the square root of 2. They cannot be expressed as fractions.

The key takeaway: if a decimal terminates or recurs, it is rational. If it neither terminates nor recurs, it is irrational.

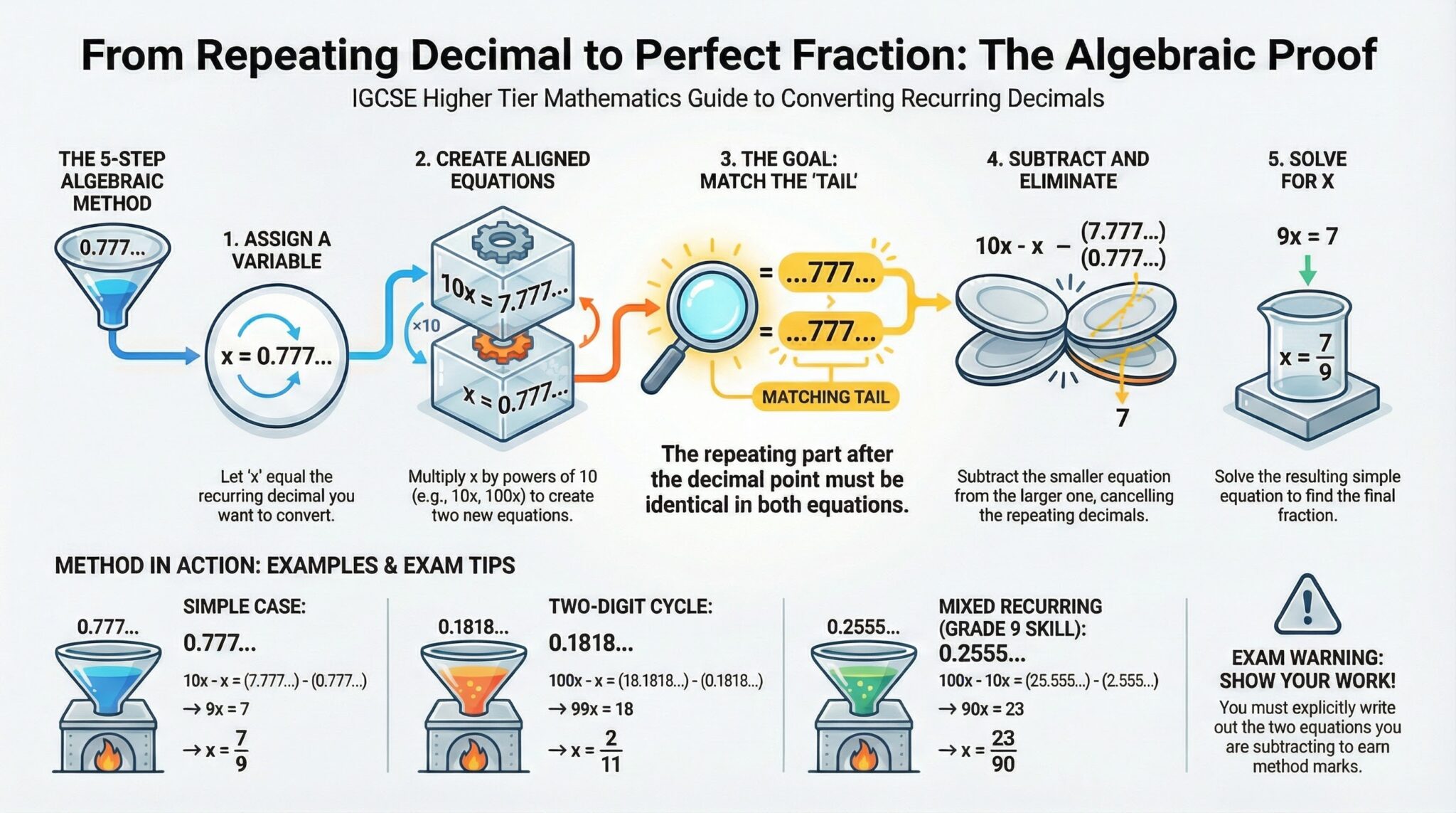
How do you convert recurring decimals to fractions?

The algebraic method is a five-step process that uses simultaneous-equation-style reasoning to eliminate the recurring digits:

1. Step 1 — Let x equal the recurring decimal. Write it out showing the repeating cycle clearly.
2. Step 2 — Identify the repeating cycle length. Count how many digits repeat. One repeating digit means you multiply by 10, two repeating digits by 100, three by 1000, and so on.
3. Step 3 — Multiply x by the appropriate power of 10 so that the repeating digits shift exactly one full cycle to the left of the decimal point.
4. Step 4 — Subtract the two equations. The recurring parts cancel, leaving a clean equation.
5. Step 5 — Solve for x and simplify the fraction fully.

For mixed recurring decimals (where only some digits after the decimal point repeat), you need two multiplications to align the repeating parts before subtracting.

Worked Examples

Common Mistakes to Avoid

Exam Tips for Recurring Decimals