IGCSE Maths: Mastering Algebraic Manipulation (Expanding and Factorising)
Algebraic manipulation is the "grammar" of mathematics. Before you can solve complex equations, simplify fractions, or graph functions, you must be able to rearrange expressions with confidence. This topic is the cornerstone of the IGCSE Algebra Hub.
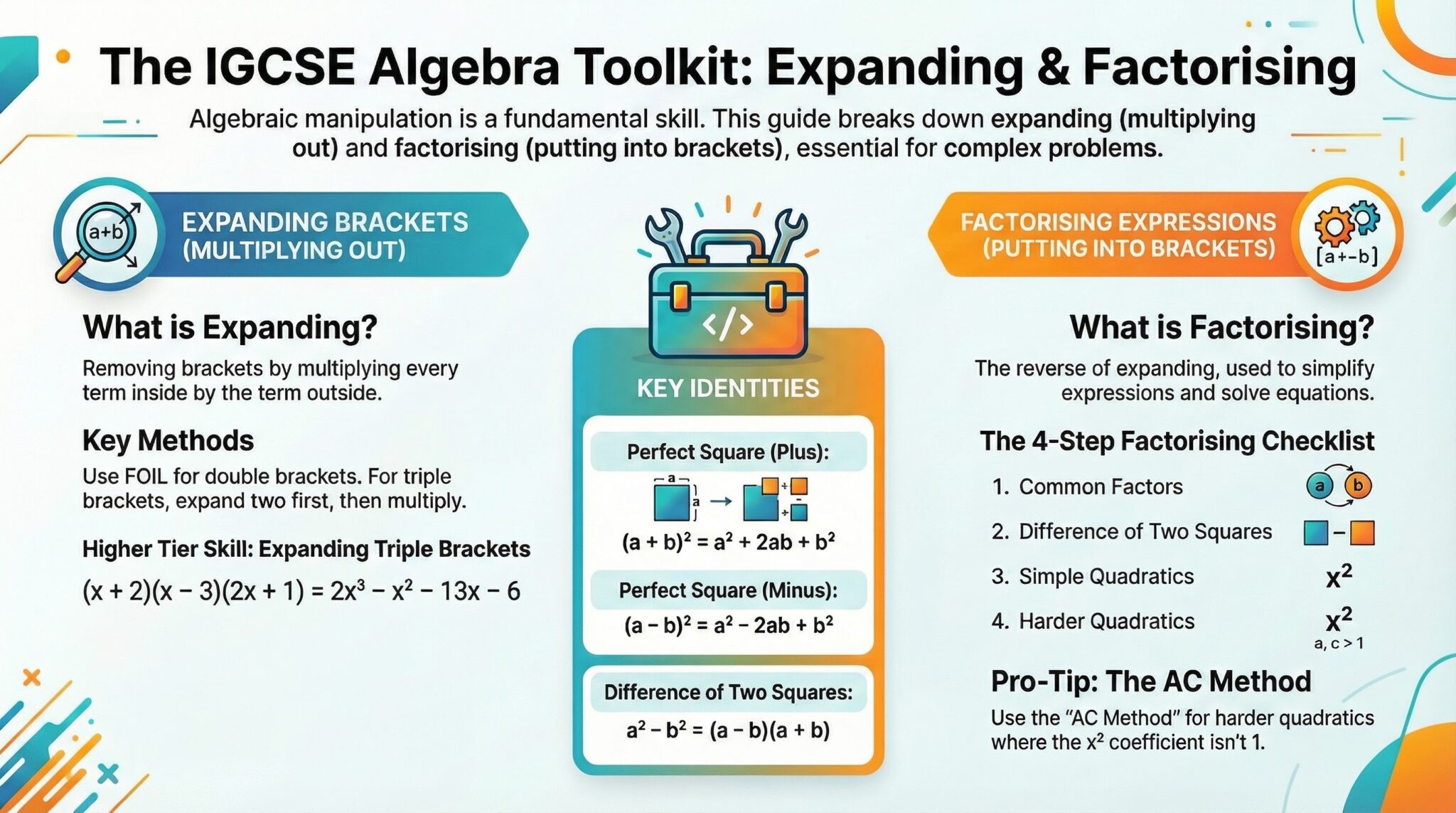
In the Edexcel IGCSE 4MA1 Higher Tier syllabus, this topic moves beyond basic brackets into "Grade 9" territory, including expanding triple brackets and factorising harder quadratics where the coefficient of \(x^2\) is greater than 1.
1. Expanding Brackets
Expanding (or "multiplying out") involves removing brackets by multiplying every term inside by the term (or bracket) outside.
Single and Double Brackets
- Single: 3x(2x - 5) = 6x² - 15x.
- Double (FOIL): (x + 3)(x - 4). Multiply First, Outer, Inner, and Last terms, then simplify.
Triple Brackets (H)
A standard Higher Tier skill. Do not try to do all three at once. Expand two brackets to form a quadratic, then multiply that result by the third bracket.
2. Factorising: The Reverse Process
Factorising is putting an expression back into brackets. You should check for these four types in order:
Type 1: Common Factors
Always look for this first. Extract the highest common factor (number and letter) from all terms.
Example: 6x² - 9x = 3x(2x - 3).
Type 2: Difference of Two Squares (DOTS)
This is a specific pattern: a squared term minus another squared term (no middle x term).
Formula: a² - b² = (a - b)(a + b)
Example: x² - 25 = (x - 5)(x + 5).
Type 3: Simple Quadratics (a = 1)
For x² + bx + c, find two numbers that multiply to make c and add to make b.
Type 4: Harder Quadratics (a > 1) (H)
For ax² + bx + c where a is not 1 (e.g., 3x² + ...), use the AC Method (Splitting the Middle Term). This is the most reliable way to ensure full marks.
Key Formulas and Identities
Memorizing these patterns will save you time and reduce errors.
| Identity Name | Formula | Example |
|---|---|---|
| Perfect Square (Plus) | (a + b)² = a² + 2ab + b² | (x + 3)² = x² + 6x + 9 |
| Perfect Square (Minus) | (a - b)² = a² - 2ab + b² | (x - 5)² = x² - 10x + 25 |
| Difference of Two Squares | a² - b² = (a - b)(a + b) | x² - 16 = (x - 4)(x + 4) |
Step-by-Step Worked Examples
Question: Expand and simplify (x + 2)(x - 3)(2x + 1).
Solution:
- Expand the first two brackets:
(x + 2)(x - 3) = x² - 3x + 2x - 6
= x² - x - 6 - Multiply by the third bracket:
(x² - x - 6)(2x + 1) - Multiply each term systematically:
Multiply x² by (2x+1): 2x³ + x²
Multiply -x by (2x+1): -2x² - x
Multiply -6 by (2x+1): -12x - 6 - Collect like terms:
2x³ + (x² - 2x²) + (-x - 12x) - 6
Answer: 2x³ - x² - 13x - 6.
Question: Factorise completely 4x² - 81y².
Methodology: Check for common factors (none). Notice both terms are squares separated by a minus.
Solution:
- Square root of 4x² is 2x.
- Square root of 81y² is 9y.
- Apply formula (a+b)(a-b):
(2x + 9y)(2x - 9y).
Answer: (2x + 9y)(2x - 9y).
Question: Factorise 3x² + 10x - 8.
Methodology: Coefficient a = 3 (greater than 1). Use the AC Method.
Solution:
- Multiply a × c: 3 × -8 = -24.
- Find factors of -24 that add to b (10):
Factors: (1, -24), (2, -12), (3, -8), (4, -6)... and their reverses.
We need +12 and -2. (12 - 2 = 10). - Split the middle term: Rewrite 10x using these numbers.
3x² + 12x - 2x - 8 - Factorise by grouping:
First pair: 3x² + 12x → 3x(x + 4)
Second pair: -2x - 8 → -2(x + 4) - Finalise: The bracket (x + 4) is common.
(3x - 2)(x + 4).
Answer: (3x - 2)(x + 4).
Real-World Application (Global Context)
Algebraic manipulation is essential in engineering for optimizing material usage and costs.
Scenario: Optimizing Packaging Volume
A manufacturer produces boxes from rectangular sheets of metal by cutting squares of side x from each corner and folding up the sides. If the original sheet is 30cm by 20cm, the volume of the box is given by:
V = x(30 - 2x)(20 - 2x)
To find the maximum possible volume (an optimization problem in calculus), an engineer must first expand this expression into a polynomial (4x³ - 100x² + 600x). Without fluency in expansion, the subsequent calculus steps are impossible.
Exam Technique and Common Pitfalls
1. The "Sign" Trap
When expanding brackets involving negatives, e.g., -3(x - 4), a very common error is writing -3x - 12. Remember your rules of directed numbers: negative × negative = positive. Correct: -3x + 12.
2. Incomplete Factorisation
If a question asks to "Factorise Completely," check if you can go further.
Example: 2x² - 50.
Partial: 2(x² - 25).
Complete: 2(x - 5)(x + 5) (Recognizing the DOTS inside).
3. Checking Your Answer
Factorisation is one of the few topics where you can guarantee your marks. Once you have an answer, expand it back out in your head. If it doesn't match the original question, you've made a mistake.
If you find yourself struggling with the logic of the AC method or sign errors, mastering advanced algebra with targeted practice is the best way to secure these high-value marks.
Summary Checklist and Next Steps
Checklist:
- [ ] I can expand single, double, and triple brackets.
- [ ] I can identify and extract common factors (e.g., 3x).
- [ ] I can factorise simple quadratics (a=1).
- [ ] I can identify and factorise the Difference of Two Squares.
- [ ] (H) I can factorise harder quadratics (a>1) using the AC method.
Next Steps:
Now that you can manipulate expressions, you are ready to apply these skills to Topic 2.2 Algebraic Fractions, where factorising is the key to simplification.