IGCSE Maths: Mastering Algebraic Fractions (H)
Algebraic fractions are simply fractions where the numerator, denominator, or both are algebraic expressions. They follow the exact same rules as numerical fractions, but with an added layer of complexity: you must be fluent in factorising.
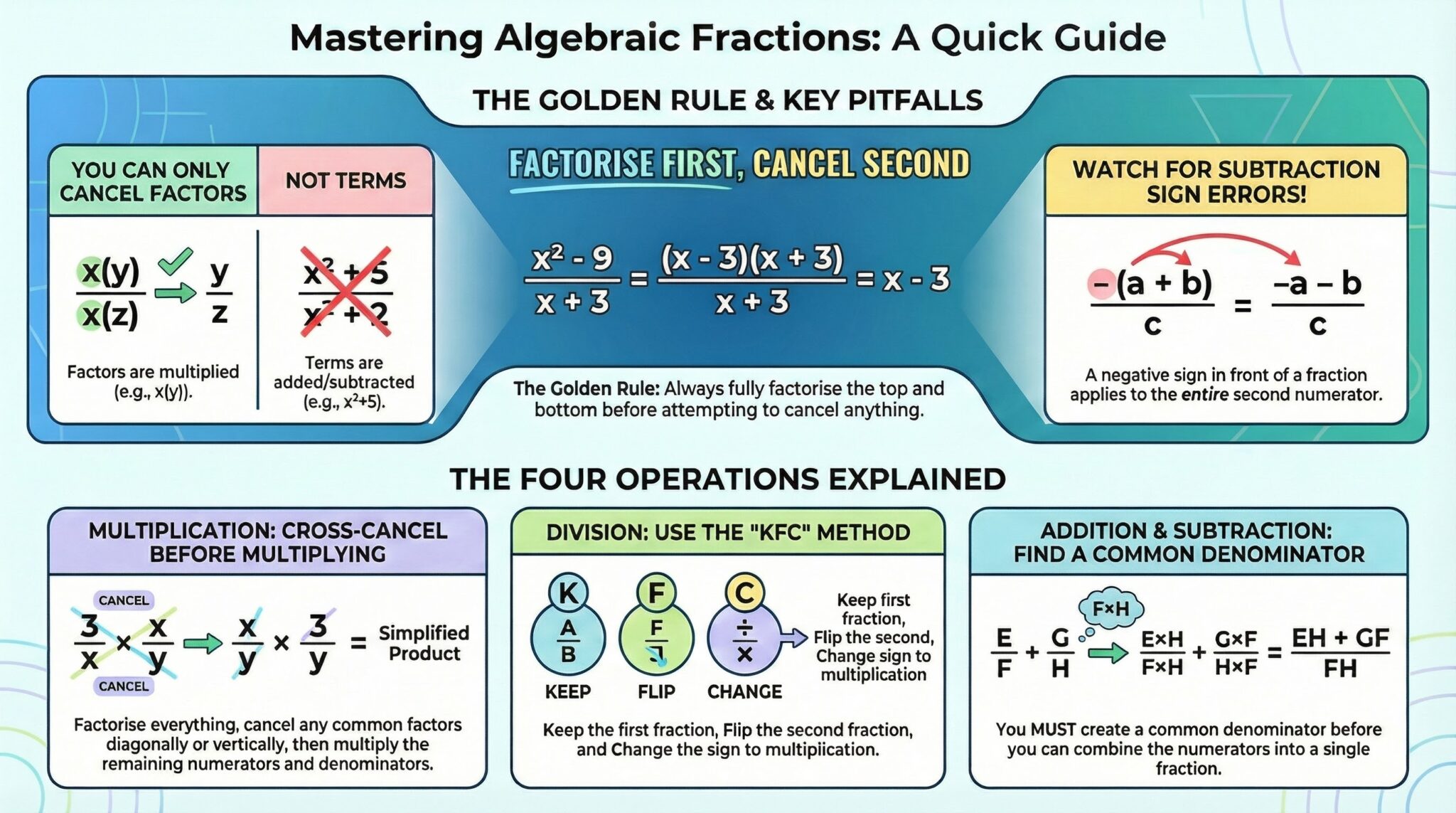
This topic is a staple of the Edexcel IGCSE 4MA1 Higher Tier exams. Mastery here is essential for solving complex equations and serves as a bridge to advanced calculus in further studies. This guide covers simplification and the four operations: adding, subtracting, multiplying, and dividing.
1. Simplifying Algebraic Fractions
The golden rule of algebraic fractions is: Factorise First, Cancel Second.
You cannot cancel individual terms that are being added or subtracted. You can only cancel factors (things that are being multiplied).
Method:
- Factorise the numerator completely (look for common factors, DOTS, or quadratics).
- Factorise the denominator completely.
- Cancel any common brackets or terms that appear on both the top and bottom.
Example: Simplify x² - 9x² + 5x + 6.
- Numerator (DOTS): (x - 3)(x + 3)
- Denominator (Quadratic): (x + 2)(x + 3)
- Cancel (x + 3): x - 3x + 2
2. Multiplying and Dividing
These are the easiest operations because you do not need a common denominator.
Multiplication
Multiply the tops (numerators) and multiply the bottoms (denominators). However, it is much more efficient to cross-cancel common factors before multiplying.
Division (KFC Method)
Just like numerical fractions, use Keep, Flip, Change.
- Keep the first fraction.
- Flip the second fraction (reciprocal).
- Change the division sign to multiplication.
- Factorise and cancel before simplifying.
3. Adding and Subtracting
This is where most students lose marks. You must have a common denominator.
Method:
- Find the Lowest Common Denominator (LCD). This is usually the product of the distinct linear factors in the denominators.
- Adjust the numerators so they are over the common denominator.
- Combine the numerators into a single expression. Be careful with subtraction signs!
- Expand and simplify the numerator. Do not expand the denominator unless asked.
Key Formulas
While there are no specific "formulas" to memorize, you must be fluent in the algebraic identities from Topic 2.1:
- DOTS: a² - b² = (a - b)(a + b)
- Perfect Squares: (a + b)² = a² + 2ab + b²
Step-by-Step Worked Examples
Question: Simplify fully 2x² - 5x - 3x² - 9.
Methodology: Factorise top and bottom separately. The top is a "Harder Quadratic" (a>1), so use the factorising quadratics method.
Solution:
- Numerator (AC Method): 2x² - 5x - 3.
Multiply to -6, add to -5 (-6, +1).
2x² - 6x + x - 3 = 2x(x - 3) + 1(x - 3) = (2x + 1)(x - 3). - Denominator (DOTS): x² - 9 = (x - 3)(x + 3).
- Combine: (2x + 1)(x - 3)(x - 3)(x + 3).
- Cancel (x - 3): 2x + 1x + 3.
Answer: 2x + 1x + 3.
Question: Simplify x3x - 6 ÷ x²x - 2.
Solution:
- KFC (Flip second fraction): x3x - 6 × x - 2x².
- Factorise: 3x - 6 becomes 3(x - 2).
- Rewrite: x3(x - 2) × x - 2x².
- Cross-Cancel:
- (x - 2) cancels with (x - 2).
- x on top cancels with one x on bottom (x² becomes x).
- Simplify: 13x.
Answer: 13x.
Question: Express as a single fraction: 4x + 2 - 32x - 1.
Methodology: The denominators are different, so multiply them to find the LCD.
Solution:
- Common Denominator: (x + 2)(2x - 1).
- Adjust Numerators:
4(2x - 1)(x + 2)(2x - 1) - 3(x + 2)(x + 2)(2x - 1). - Combine Numerators (Watch the negative!):
4(2x - 1) - 3(x + 2) = 8x - 4 - 3x - 6. - Simplify Numerator: 5x - 10.
- Final Fraction: 5x - 10(x + 2)(2x - 1).
- Check if numerator factorises (5(x-2)) to cancel further. No common factors here.
Answer: 5(x - 2)(x + 2)(2x - 1).
Real-World Application (Global Context)
Algebraic fractions are fundamental in engineering, specifically when dealing with parallel circuits in electronics.
Scenario: Parallel Resistors
The total resistance R of two resistors R₁ and R₂ connected in parallel is given by the formula:
1R = 1R₁ + 1R₂
To make this useful (making R the subject), an engineer must add the algebraic fractions on the right-hand side:
- Common Denominator: R₁R₂.
- Add: R₂ + R₁R₁R₂.
- Invert: R = R₁R₂R₁ + R₂.
This simplified algebraic fraction allows engineers to quickly calculate total resistance without performing multiple reciprocal calculations.
Exam Technique and Common Pitfalls
1. The "Fake Cancellation" Error
This is the most common mistake. In the fraction x² + 5x² + 2, you cannot cancel the x² terms. They are "glued" to the other numbers by the plus sign. You can only cancel if you have x²(y)x²(z).
2. Sign Errors in Subtraction
When subtracting fractions like in Example 3, the negative sign applies to the entire second numerator.
Incorrect: 4(2x - 1) - 3(x + 2) → 8x - 4 - 3x + 6.
Correct: 8x - 4 - 3x - 6.
3. Leaving the Denominator Expanded
Usually, you do not need to expand the denominator (e.g., (x+2)(2x-1)) in the final answer. Leaving it in brackets is often preferred and saves time.
Mastering these techniques is crucial for mastering high-level algebra and securing the top marks in the IGCSE exam.
Summary Checklist and Next Steps
Checklist:
- [ ] I know to factorise before simplifying any fraction.
- [ ] I can multiply algebraic fractions by multiplying tops and bottoms (and cross-canceling).
- [ ] I can divide algebraic fractions using the KFC method.
- [ ] I can add and subtract algebraic fractions by finding a common denominator.
- [ ] I am careful with negative signs when combining numerators.
Practice Resources
Mastering algebraic fractions requires consistent practice. Use our dedicated worksheet to test your skills on simplifying, multiplying, dividing, and adding algebraic fractions.
Download Topic Worksheet: Algebraic Fractions (Simplifying & Operations)
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
Now that you can manipulate algebraic fractions, the next logical step is Topic 2.3 Formulae, where you will use these skills to rearrange complex formulas involving fractions and roots.