The Ultimate Guide to IGCSE Algebra: Equations, Formulae, and Identities
Algebra is the language of mathematics. In the Edexcel International GCSE (IGCSE) Mathematics A (4MA1) syllabus, Topic 2: Equations, Formulae, and Identities is the heavyweight champion, often accounting for over 30% of the available marks.
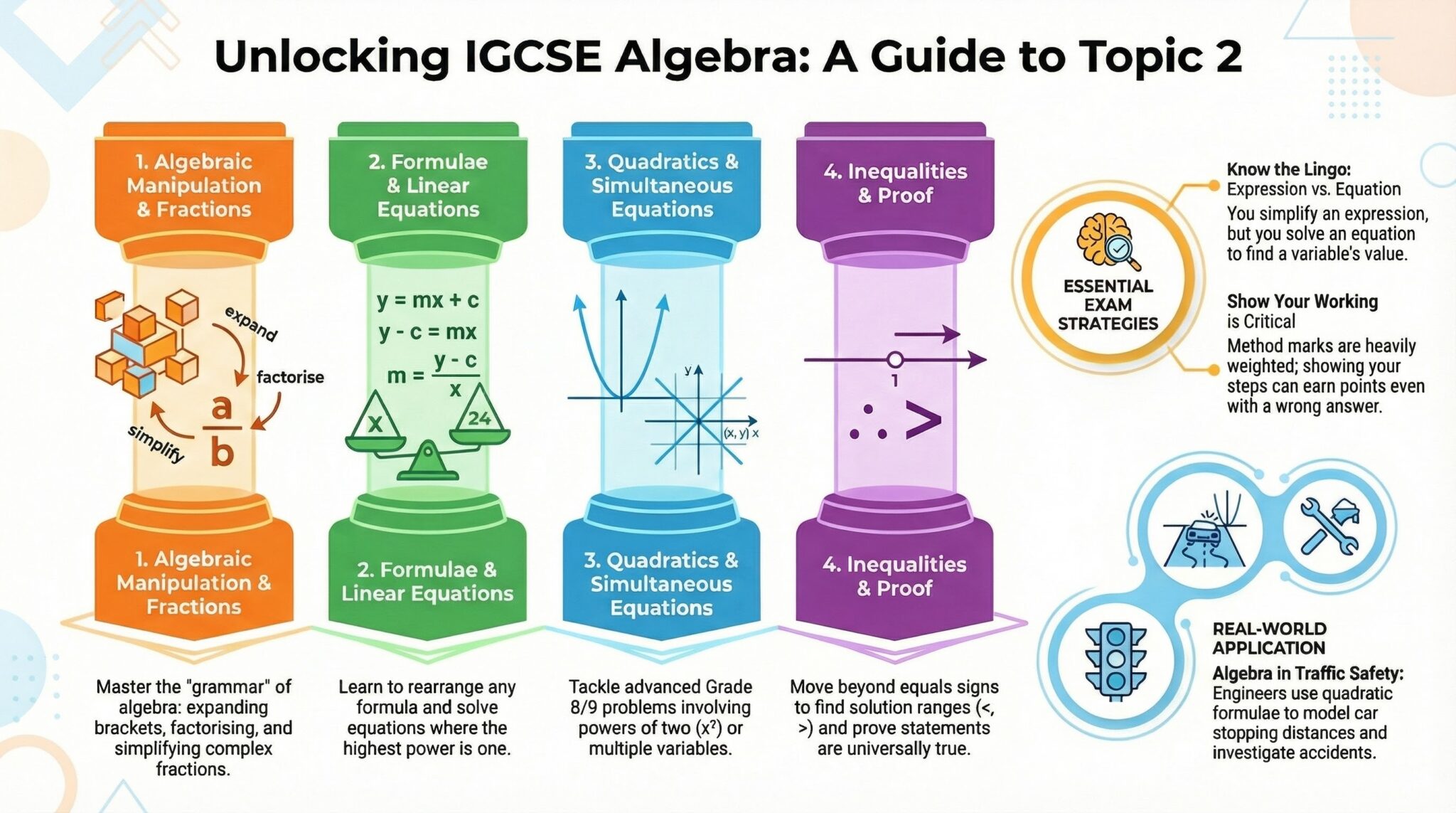
This guide serves as your central hub for mastering Algebra. It generalizes the rules of the Number System foundations to provide the toolkit needed for solving abstract problems. We have broken down the syllabus into four logical pillars.
Video Masterclass: The Complete Topic 2 Strategy & Grade 9 Toolkit
Deep Dive: The Structure of IGCSE Algebra
Click through to the detailed guides below for deep practice on specific skills.
1. Algebraic Manipulation and Fractions (2.1 – 2.2)
Before you can solve complex equations, you must be fluent in manipulating expressions. These skills are the grammar of the algebraic language.
2.1 Algebraic Manipulation
This involves expanding brackets and factorising expressions—essentially the reverse of each other.
- Expanding: Multiplying terms out, including double brackets (quadratics) and triple brackets.
- Factorising: Putting terms back into brackets using common factors, difference of two squares, and quadratic factorization (including hard quadratics where the coefficient of x² > 1).
2.2 Algebraic Fractions (H)
One of the most challenging topics for students. It combines the rules of numerical fractions with factorisation.
- Simplifying: You cannot simply "cancel" terms; you must factorise the top and bottom first.
- Operations: Adding, subtracting, multiplying, and dividing algebraic fractions.
2. Formulae and Linear Equations (2.3 – 2.4)
These topics deal with linear relationships (powers of 1) and the manipulation of formulas.
2.3 Formulae
Formulae allow us to calculate values. The key skill here is rearranging (changing the subject).
- Substitution: Replacing variables with numbers (respecting BIDMAS and negative numbers).
- Rearranging (H): Isolating a variable when it appears twice, or is trapped inside a square root or fraction.
2.4 Linear Equations
Solving equations to find the value of x, including equations with brackets and fractions.
Read the detailed guide on Linear Equations →3. Quadratics and Simultaneous Equations (2.5 – 2.6)
This is where the difficulty ramps up to Grade 8/9 levels.
2.5 Simultaneous Equations
Finding the values of two variables (x and y) that satisfy two equations at the same time.
- Linear/Linear: Solved by Elimination or Substitution. Represents the intersection of two straight lines.
- Linear/Quadratic (H): Solved by Substitution. Represents a line intersecting a curve.
2.6 Quadratic Equations
Equations where the highest power is 2 (ax² + bx + c = 0). These are fundamental to Higher Tier maths.
- Factorisation: Finding the two brackets.
- The Quadratic Formula (H): Using the formula when the answers are not integers (surds/decimals).
- Completing the Square (H): A powerful technique for solving quadratics and finding turning points of graphs.
4. Inequalities and Proof (2.7 – 2.8)
These topics deal with ranges of values and logical rigor.
2.7 Inequalities
Dealing with "greater than" (>) or "less than" (<) relationships.
- Linear Inequalities: Solving like equations, but flipping the sign if dividing by a negative.
- Quadratic Inequalities (H): Finding the range of values between (or outside) the roots of a quadratic.
2.8 Algebraic Proof (H)
Using algebra to demonstrate that a statement is mathematically true for all numbers (e.g., "Prove that the sum of three consecutive integers is a multiple of 3").
Read the detailed guide on Algebraic Proof →Synthesized Worked Example (Grade 9 Level)
High-tariff exam questions often combine multiple algebraic skills, such as algebraic fractions and quadratic equations.
Solve the equation:
3x + 2 + 42x - 1 = 2
Show clear algebraic working.
SolutionStep 1: Eliminate the fractions (Common Denominator).
Multiply every term by (x + 2)(2x - 1):
3(2x - 1) + 4(x + 2) = 2(x + 2)(2x - 1)
Step 2: Expand the brackets.
LHS: 6x - 3 + 4x + 8 = 10x + 5
RHS: Expand double brackets first: 2[2x2 - x + 4x - 2] = 2[2x2 + 3x - 2] = 4x2 + 6x - 4
Equation: 10x + 5 = 4x2 + 6x - 4
Step 3: Rearrange to form a quadratic = 0.
Subtract 10x and 5 from both sides:
0 = 4x2 - 4x - 9
Step 4: Solve the Quadratic.
This does not factorise easily. Use the Quadratic Formula: a=4, b=-4, c=-9.
x = -(-4) ± √((-4)2 - 4(4)(-9))2(4)
x = 4 ± √(16 + 144)8 = 4 ± √1608
Answer: x = 1 + √102 or x = 1 - √102
Real-World Application (Global Context)
Algebraic formulae allow us to model the physical world, from the trajectory of a football to the braking distance of a car.
Scenario: Traffic Safety Analysis
A traffic safety engineer models the stopping distance (d) of a car using the formula:
d = 0.7v + 0.06v2
Where v is the speed in m/s. The term 0.7v represents reaction time distance, and 0.06v2 represents braking distance. If a car leaves a skid mark showing it stopped in exactly 80 meters, the engineer must solve the quadratic equation to determine if the driver was speeding. This is a daily application of quadratics in forensic accident reconstruction.
Exam Strategies for IGCSE Algebra
1. Equation vs. Identity vs. Expression
Know the difference to avoid confusion:
- Expression: A collection of terms (e.g., 2x + 5). No equals sign. You can simplify it.
- Equation: Two expressions equal to each other (e.g., 2x + 5 = 15). You can solve it.
- Identity: True for ALL values of x (denoted by ≡). E.g., 2(x + 3) ≡ 2x + 6.
2. "Show Your Working" is Critical
In solving quadratics or simultaneous equations, method marks are heavily weighted. If you use a calculator to find the roots but show no algebraic working (factorising or formula substitution), you will likely score zero.
3. Check Your Answers
Algebra has a built-in checking mechanism. If you solve an equation and get x = 4, substitute 4 back into the original equation. If it balances, you know you are correct.
Algebra makes up a massive portion of the exam marks. If you are aiming for a Grade 8 or 9, expert algebra tuition can help you master the nuances of proof and complex equations.
Summary and Next Steps
Mastering Topic 2 is the turning point for many IGCSE students. It moves you from arithmetic into abstract reasoning. Use this hub to navigate through each sub-topic, ensuring you are comfortable with both the mechanical skills (like expanding brackets) and the logical skills (like forming equations).
Practice with IGCSE Maths Worksheets
Mastering algebra requires consistent practice. Consolidate your learning across all these sub-topics with our comprehensive library of worksheets and model answers.
Get Free IGCSE Edexcel Maths Worksheets & Answers
What's Next?
Once you have mastered algebraic manipulation, you are ready to visualize these concepts in Topic 3: Functions and Graphs, where equations turn into lines, curves, and gradients.