IGCSE Maths: Degree of Accuracy, Bounds, and Error Intervals (H)
In the real world, no measurement is ever perfectly exact. Whether measuring the speed of a car or the thickness of a sheet of paper, there is always a limit to our precision. In the IGCSE Number System syllabus, understanding this uncertainty is critical.
This guide covers Topic 1.9 Degree of Accuracy, taking you from basic rounding and estimation to the advanced concept of Upper and Lower Bounds. Questions on calculating with bounds are frequent "Grade 8/9" discriminators that test your logical reasoning as much as your arithmetic.
1. Rounding and Estimation
Before diving into bounds, you must be flawless with the basics of precision.
Rounding: Decimal Places vs. Significant Figures
- Decimal Places (dp): Counts digits after the decimal point. Used to fix precision relative to whole numbers (e.g., money is always 2 dp).
- Significant Figures (sf): Counts the number of digits that carry meaning, starting from the first non-zero digit. Used for scientific precision.
Estimation (The "One Sig Fig" Rule)
IGCSE estimation questions ask you to "Estimate the value of..." without using a calculator.
- Rule: Round every number in the calculation to 1 significant figure (1 sf) before calculating.
- Example: Estimate 41.2 × 19.80.49.
- Round: 40 × 200.5.
- Calculate: 8000.5 = 1600. (Dividing by 0.5 is the same as multiplying by 2).
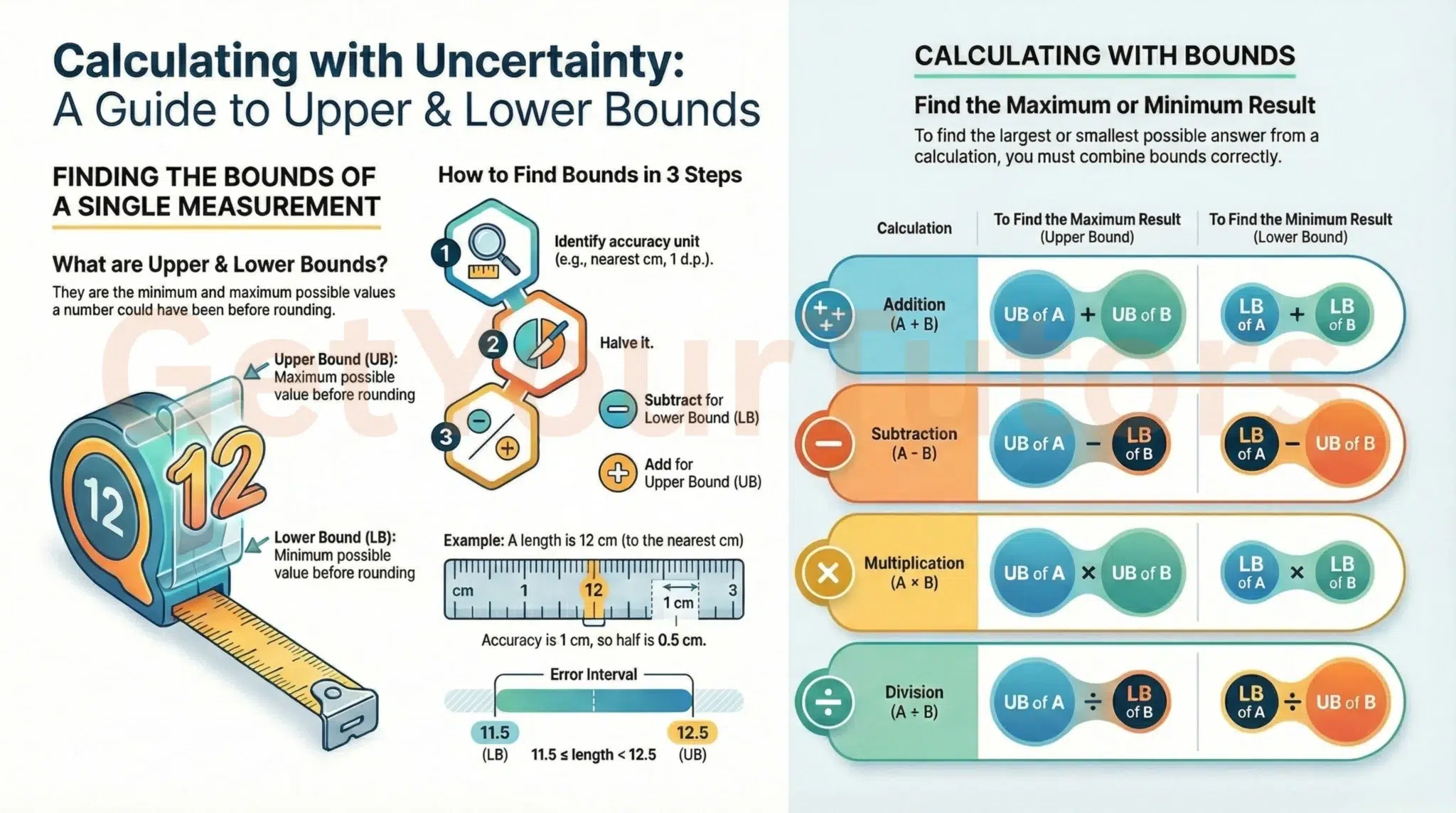
2. Limits of Accuracy: Upper and Lower Bounds (H)
When a measurement is rounded, the true value lies within a range known as the Error Interval.
Finding the Bounds (The Half-Unit Rule)
To find the bounds, take the degree of accuracy, divide it by 2, and add/subtract this from the rounded value.
- Identify the unit of accuracy:
- "Correct to the nearest 10" → Unit = 10.
- "Correct to 1 decimal place" → Unit = 0.1.
- "Correct to 3 significant figures" → Determine the place value of the last digit.
- Calculate the tolerance (Half-Unit): Unit ÷ 2.
- Apply:
- Upper Bound (UB): Rounded Value + Tolerance
- Lower Bound (LB): Rounded Value - Tolerance
Error Intervals
We express the range of possible values (x) using inequalities. Note the strict inequality (<) for the Upper Bound.
LB ≤ x < UB
Example: A length L is 12 cm to the nearest cm.
11.5 ≤ L < 12.5
3. Calculations with Bounds (The Grade 9 Skill)
The hardest questions ask you to calculate quantities (like Speed, Area, or Density) using rounded values. You must decide logically whether to use the UB or LB to get the Maximum or Minimum possible result.
The Logic Table
| Operation | To Find Maximum | To Find Minimum |
|---|---|---|
| Addition (A + B) | UBA + UBB | LBA + LBB |
| Subtraction (A - B) | UBA - LBB (Start Big - Subtract Small) |
LBA - UBB (Start Small - Subtract Big) |
| Multiplication (A × B) | UBA × UBB | LBA × LBB |
| Division (A ÷ B) | UBA ÷ LBB (Big Numerator ÷ Small Denominator) |
LBA ÷ UBB (Small Numerator ÷ Big Denominator) |
Crucial Insight: For subtraction and division, the bounds are "crossed." To maximize a division, you need the largest possible number on top divided by the smallest possible number on the bottom.
Step-by-Step Worked Examples
Question: A rectangular card measures 12 cm by 8 cm, correct to the nearest cm. Calculate the upper bound for the perimeter.
Solution:
- Find Bounds for dimensions:
- Length (12): LB=11.5, UB=12.5.
- Width (8): LB=7.5, UB=8.5.
- Calculate Max Perimeter:
Perimeter = 2 × (Length + Width)
Max Perimeter = 2 × (12.5 + 8.5)
= 2 × 21 = 42 cm.
Answer: 42 cm.
Question: F = ma.
m = 20 kg (correct to 1 significant figure).
a = 5.2 m/s² (correct to 2 significant figures).
Calculate the Upper Bound of Force F.
Methodology: Max Force = Max Mass ÷ Min Acceleration.
Solution:
- Find Bounds for m (The 1 sf Trap):
- The number is 20. The first significant figure is '2', which is in the tens column.
- Unit = 10. Tolerance = 5.
- mUB = 20 + 5 = 25. (Note: Many students incorrectly say 20.5. Check the place value!)
- Find Bounds for a:
- Rounded to 0.1. Tolerance = 0.05.
- aLB = 5.2 - 0.05 = 5.15.
- Calculate:
Fmax = 255.15 = 4.85436...
Answer: 4.85 N (3 sf).
Question: V = xy.
x = 4.3 (correct to 1 d.p.)
y = 2.15 (correct to 2 d.p.)
Calculate the value of V to a suitable degree of accuracy. Justify your answer.
Methodology: Calculate both the Max and Min values of V. Round them until they match.
Solution:
- Find Bounds:
- x: 4.25 ≤ x < 4.35
- y: 2.145 ≤ y < 2.155
- Calculate Max V (UBx ÷ LBy):
Vmax = 4.352.145 = 2.02797... - Calculate Min V (LBx ÷ UBy):
Vmin = 4.252.155 = 1.97215... - Compare and Round:
- Vmax = 2.02...
- Vmin = 1.97...
- Do they match to 2 decimal places? No (2.03 vs 1.97).
- Do they match to 1 decimal place? No (2.0 vs 2.0—wait, 1.97 rounds to 2.0).
- Do they match to 2 significant figures? Yes. Both round to 2.0.
- Justification: Both the Upper and Lower bounds round to 2.0 (to 2 s.f.).
Answer: 2.0.
Real-World Application (Global Context)
Bounds are vital in engineering and high-performance mechanics, known as Tolerance.
Scenario: F1 Racing Pistons
In a Formula 1 engine, the piston must fit perfectly inside the cylinder.
- Cylinder Diameter: 98.05 mm ± 0.01 mm.
- Piston Diameter: 98.02 mm ± 0.01 mm.
To ensure the engine doesn't seize (piston too big) or lose compression (piston too small), engineers calculate the Clearance using bounds.
- Minimum Clearance = Cylinder Min (LB) - Piston Max (UB).
- If this calculation results in a negative number, the piston won't fit, and the engine will fail. This mathematical assurance is crucial for safety and performance.
Exam Technique and Common Pitfalls
1. The "Truncation" Trap
Usually, bounds are ± half a unit. However, if a question says "truncated to 1 decimal place" (just cut off), the logic changes.
- Truncated 4.3: The interval is 4.3 ≤ x < 4.4.
- Rounded to 4.3: The interval is 4.25 ≤ x < 4.35.
- Always check if the question says "rounded" or "truncated".
2. Discrete vs. Continuous Data
- Continuous (Measurement): 12 cm (nearest cm) → UB = 12.5.
- Discrete (Counting): 12 people (nearest person) → You cannot have 12.5 people.
- Tip: For Edexcel calculation questions involving formulas (like V=I × R), treat all variables as continuous bounds unless explicitly stated otherwise.
3. Showing Working
For "Suitable Degree of Accuracy" questions, you must write down the full decimal expansions of both the Upper and Lower bound calculations before rounding them. This is a common place to lose marks, so mastering high-tariff exam questions involves showing every step clearly.
Summary Checklist and Next Steps
Checklist:
- [ ] I can identify the degree of accuracy (e.g., nearest 10, 0.1, or 3 sf).
- [ ] I can calculate the error interval (LB ≤ x < UB).
- [ ] I know the logic rules for calculating Max/Min for subtraction and division.
- [ ] I can solve "Suitable Degree of Accuracy" questions by comparing UB and LB results.
Practice Resources
Mastering upper and lower bounds requires logical thinking and practice. Use our dedicated worksheet to test your skills on these complex error interval calculations.
Download Topic Worksheet: Accuracy, Bounds & Error Intervals
Looking for more practice? Access our complete library of IGCSE maths worksheets and answers:
Get Free IGCSE Edexcel Maths Worksheets & Answers
Next Steps:
You have now completed the standard numerical topics! The next topic deals with very large and small numbers: Topic 1.10 Standard Form, where you will apply index laws and precision to scientific notation.